长激光中的退相干和湍流源
专家视点
几个世纪以来,光的相干特性一直吸引着研究人员,随着激光的发现,许多设备已经将相干应用于从通信网络到计量等行业,包括用于光学通信的马赫-曾德尔调制器、用于光学相干断层扫描的扫频源激光器、用于高精度计量的光学频率梳或者具有prad/s分辨率分数的环形激光陀螺仪。在此,Amy Roche等人实验和理论研究了高多模激光器开启瞬态期间光的动力学和统计特性,其中往返时间比增益介质的时间尺度大几个数量级。在这个长延迟极限中,光子统计从热分布到泊松分布的普遍演化涉及功率下降的出现。这些相干结构连接具有不同光学频率的固定激光发射域。此外,它们发射以不同速度传播的强度爆发且根据腔色散符号,它们可能与其他相干结构碰撞,从而导致整体湍流动力学。动力学由延迟微分方程很好地建模,从中计算了每次往返时的激光相干时间演变,并量化了相干结构之间碰撞引起的退相干。这项研究揭示了在瞬态积累的早期往返中,通过相干结构的形成和碰撞,驱动长激光从稳定的、低于阈值的运转演变为湍流状态的普遍机制。所用激光系统由封装在无源光纤腔中的半导体增益介质组成,其往返行程远大于增益介质的时间尺度。这种长腔允许单向场传播。长腔激光器与通常用于光学相干断层扫描的傅立叶域锁模激光器紧密相连。特别是,考虑的装置用于描述限制这些光源相干性的调制不稳定性的出现。由于长环形腔和点状半导体增益介质,能够在激光开启期间记录和分析每次往返中场的相位和强度变化,并重建相干的演变。结果表明,在第一次往返过程中,激光强度的增强以功率下降的形成为特征。在几十次往返之后,这些功率下降的最大数量消失了,光子统计向泊松统计放松。然而,它们中很少有像复Ginzburg-Landau方程所描述的那样,存活下来并产生类似于暗孤子或Nozaki Bekki空穴的相干结构。在正常的色散状态下,这些相干结构,称之为空穴,以恒定的速度传播,而它们的核心发出衰减强度的爆发,传播速度比空穴更快。在反常色散状态下,空穴发射的强度爆发可以达到并改变前一个空穴的动力学,从而导致空穴的混沌轨迹。空穴之间的这种相互作用类似于缺陷介导的湍流,是在反常色散区工作的长激光器中相干退化的主要来源。这项研究提供了关于这些状态建立的实验和理论描述,这些状态在复Ginzburg-Landau方程中是典型的,因此在自然界中普遍存在。该工作发表在Physical Review Letters上。

Amy Roche, Svetlana Slepneva, Anton Kovalev, Alexander Pimenov, Andrei G. Vladimirov, Massimo Giudici, Mathias Marconi, and Guillaume Huyet, Decoherence and Turbulence Sources in a Long Laser, PHYSICAL REVIEW LETTERS 131: 053801 (2023).
几个世纪以来,光的相干特性一直吸引着研究人员,随着激光的发现,许多设备已经将相干应用于从通信网络到计量等行业,包括用于光学通信的马赫-曾德尔调制器、用于光学相干断层扫描的扫频源激光器、用于高精度计量的光学频率梳或者具有prad/s分辨率分数的环形激光陀螺仪。
无论是在稳态还是瞬态中,单模激光器的相干特性都得到了深入的研究。在阈值以下,光子统计遵循热分布,其中相干时间与增益带宽成反比。在阈值以上,光子数按泊松统计量分布且相干时间与肖洛-汤斯线宽成反比。在纳米激光器的背景下,单模激光相干性最近引起了人们的关注,在纳米激光器中可以出现非琐碎的光子统计且可以设计高自发发射因子,例如产生无阈值激光器。
在多模激光器中,有源腔模式之间的相位关系由色散和非线性之间的相互作用决定,这可能导致相干结构的产生或完全退相干输出(诸如光学湍流)的出现。在研究暗孤子或Nozaki-Bekki空穴等相干结构的多模激光谐振器的纵向维度中已经观察到湍流。近年来,光学湍流的分析已经转移到集成光学领域。由于半导体材料中激光场的相幅耦合引起的相位湍流,集成半导体环形激光器可以使用非常低的泵浦功率进入光频梳状态。根据色散符号的不同,相同的器件也可以在Nozaki-Bekki空穴状态下工作。虽然时空激光不稳定性通常使用偏微分方程来建模,例如复金兹堡-朗道方程,但长激光系统的动力学可以使用延迟微分方程很好地建模。特别是,实现了延迟微分方程模型可以表现出局部结构以及对流和调制的不稳定性。长腔激光器显示在正常色散状态下工作稳定,而在反常色散状态下则存在调制不稳定性。在超过阈值的长激光器的静止运行中,相干结构和湍流已经得到了深入的研究;然而,关于这些激光器在开启瞬态过程中,当泵浦参数突然使激光超过阈值时向湍流过渡的信息仍然很少。
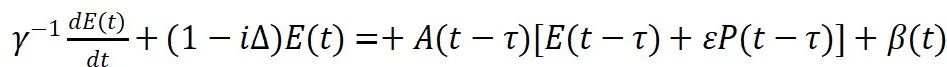
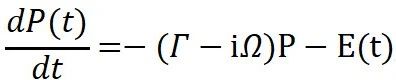
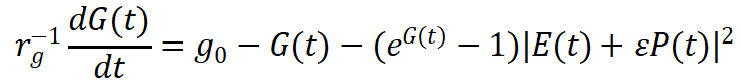
以及
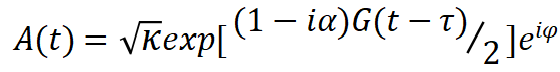
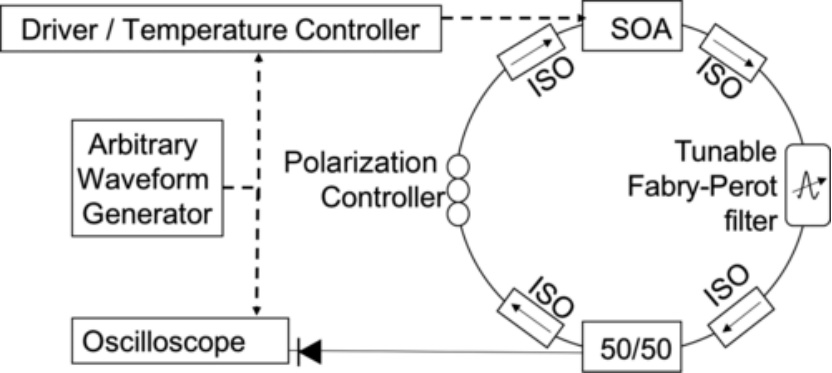
图1 具有环形光纤腔的半导体激光器的实验装置。ISO: 光纤光学隔离器。一半的激光功率用于检测。
图2的上半部分描述了实验观察到的(a)和数值计算得到的(b)激光开启瞬态的前十次往返。自发发射,当泵浦电流增加时,由半导体光放大器发出,在每个往返后被再度放大。因此,激光强度在每个往返期间逐步增加,并在几个往返后达到稳态值。激光在更长的时间内仍然表现出大幅振荡,为了进一步了解这一动态,使用时空图表示了前50次往返中激光输出的演变,如图2(c)和2(d)所示。这些图表可以在一个比腔体往返时间短的时间窗口内可视化强度的往返演变。图2(c)揭示了两种类型的功率衰退现象。第一类型(用红色箭头表示)出现在开启瞬态的第一次往返中,并在约25个往返后消失。第二类型的功率衰退现象(用黑色箭头表示)持续的往返次数更多且具有比第一类型更大的周期性。这意味着第一类型的功率消失现象的群速度比第二类型的大。通过数值积分等式,可以在图2(d)的时空图中再现这些功率消失现象,这表征了开关开启瞬态的初始阶段。
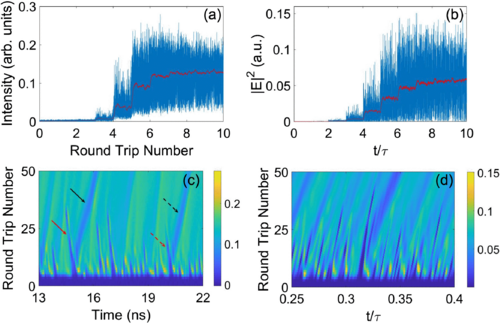
图2 (a) 半导体光放大器开启后前10次往返的强度实验时间轨迹(往返0),以12 GHz带宽(蓝色)记录,并通过数值滤波降至100 MHz(红色)。(b)泵浦开启后前10次往返激光强度的模拟时间轨迹:在全模拟带宽内(蓝色),滤波后降至100 MHz(红色)。(c) 前50次往返在9 ns时间窗内激光强度时间轨迹的二维实验图。箭头表示两种不同类型的断电结构。(d) 前50次往返期间激光强度的数值计算演变。
长腔激光开启的初始阶段可以描述为噪声再生的迭代过程。腔内滤波器的带宽决定了热噪声初始条件的带宽。每次往返后,随着激光强度的再次放大,统计波动被修正。为了描述这种行为,可以简化等式。描述每次往返后激光强度演变的一维图pn=|E(nτ)|2,从数值和实验数据可以计算出激光导通过程中激光强度概率分布函数的演变,如图3所示。这些激光强度概率分布函数的演变表现出与在单个纵向模式激光的开关中观察到的相似的行为,因为它们在发展成宽钟形分布(第16次往返)之前显示出第一次往返的常规热统计数据。另一方面,图3中所示的激光强度概率分布函数由于持续存在功率衰退,呈现出向低强度方向的长尾。
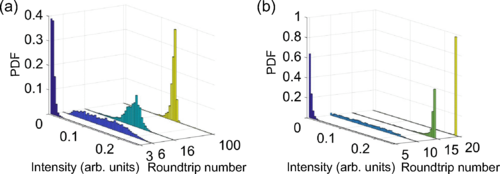
图3 实验(a)和数值(b)激光开启期间连续往返激光强度的概率分布。利用一维强度图得到了数值直方图。
为了进一步了解这些长时间的衰退的作用,研究人员测量了在导通瞬态过程中电场的时间演变。图4显示了往返次数为5 ns,15 ns和500 ns的20 ns时间窗内激光强度和电场的时间演变。这些时间序列是从图2所示的接通实现中获得的,不同往返的时间窗口以图2(c)和图4(b)中左黑色箭头所标识的功率衰退为中心。
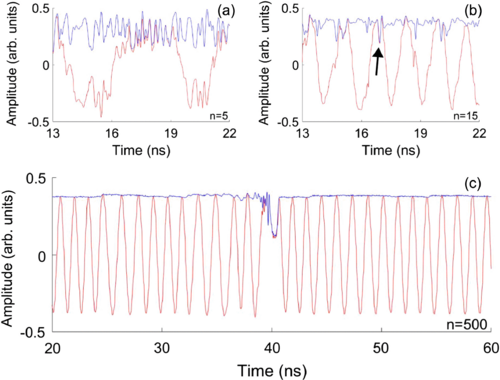
图4 往返5 (a)、15 (b)和500 (c)次时激光电场(红色)和强度(蓝色)的实验时间轨迹。图b中的箭头表示在第一次往返时出现的图2(c)中左黑色箭头所标记的落差位置。
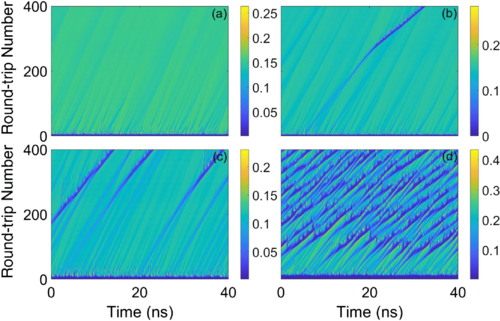
图5 不同泵浦功率和工作波长下的激光强度图。(a),(b) 在1310 nm(正常色散)下,对于P=1.6*Pth得到的两种不同的瞬态累积。(c) P=1.2*Pth, 在1310 nm处滤波(正常色散)。(d) P=1.2*Pth, 在1360 nm处滤波(反常色散)。
对于较低的注入电流,观察到更多的功率衰退持续存在,并形成几个空穴,如图5(c)所示。每个空穴的动力学与在较高注入电流下观察到的动力学相似,即它发出以较大速度传播的强度爆发。在这种状态下,这些爆发不会与其他空穴相互作用,因为它们一旦从空穴中射出就会迅速衰减。如图5(d)所示,当激光器工作在反常色散区(腔内滤波器设置为1360 nm)时,情况发生了巨大变化。在这种情况下,每次往返的功率衰退次数要大得多且每个空穴发射的辐射到达并改变了前一个空穴的动力学,从而导致空穴的混沌轨迹。这种行为构成了缺陷介导湍流中的一种新型动力学。
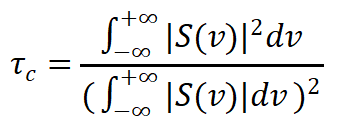
图6 由方程的数值积分得到激光强度的数值图。(1) -(3),以匹配图5所示的实验数据。计算了零色散区(ε=0),g0=1.6g0,thr (a),(b), g0=1.2g0,thr(c)和反常色散区(d), g0=1.2g0,thr, ε=1.6, Ω=30.4 GHz, Γ=15.2 GHz的分布图。
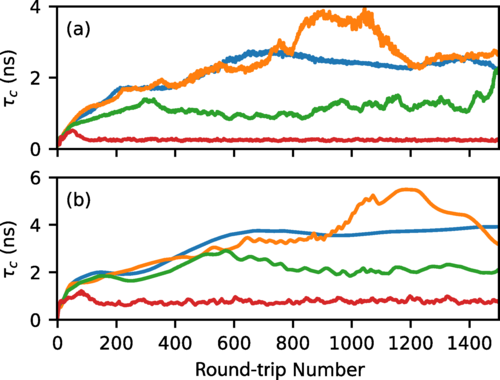
图7 相干时间作为往返次数的函数。(a) 实验。瞬态导致图5(a)所示情况下的无液滴(蓝色),图5(b)所示情况下的单液滴(橙色),图5(c)所示情况下的多液滴(绿色),图5(d)所示情况下异常色散区缺陷介导的湍流(红色)。(b) 理论。对图6中与实验相同的模拟瞬态计算相干时间。
总之,研究人员提出了一个长激光器的开启过程中强度和相位的往返解析演化,从而揭示了相干结构和湍流形成的普遍机制。研究发现,在第一次往返中由热统计到泊松统计的转变与功率衰退存在密切相关。这些功率衰退在多次往返后可能仍然存在且可以形成相干结构或孔洞。这些结构会发射强爆发,其传播速度比空穴更快。在反常色散区域,通过这些突发与其他孔洞的多次碰撞,湍流就会产生,起到一种时间退相干的机制。这项研究提供了对动力系统朝向相干结构和湍流状态的瞬态演化的首次详细研究。除了长腔激光器外,这项发现也可能与大类别的自然动力系统有关。
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。





