Zernike面型--简介
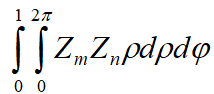
当m≠n时,其积分的值为0
当m=n时,其积分的值不为0
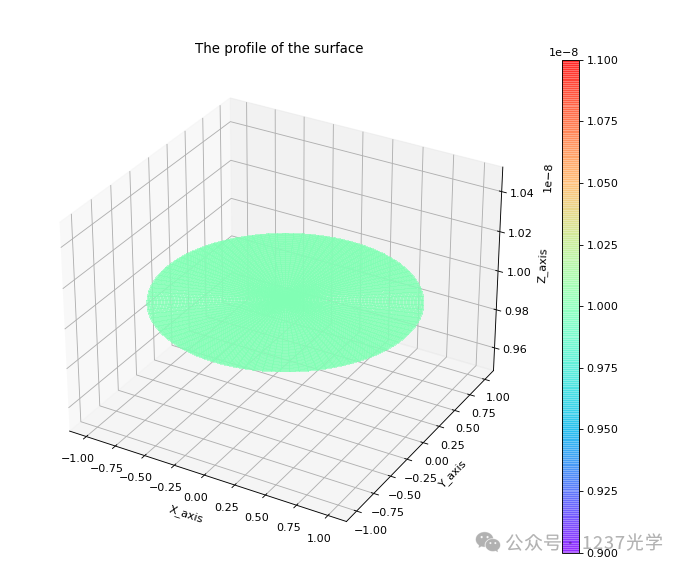
Z1--Piston
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。
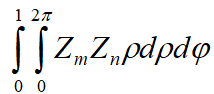
当m≠n时,其积分的值为0
当m=n时,其积分的值不为0

Z1--Piston
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。