Menu 

Menu
  1. 首页
  2. 产品应用
  3. 相位型SLM实现复振幅调制的方法

相位型SLM实现复振幅调制的方法

在光场调控的过程中，SLM是使用较为普遍的光学设备，一般情况下，对于相位型SLM，其只能对光场的相位进行调控，但实际上我们也可以通过对相位的调控来调控光的振幅，从而对光场的振幅和相位同时调控。
假设我们要实现的光场复振幅为

相位型SLM实现复振幅调制的方法

其中A和\Psi分别表示光场的振幅和相位，我们同样基于加载全息光栅的方法来实现复振幅调控。不同于我们之前使用的光栅（参考：通过SLM产生涡旋光），这里光栅的透过率函数可写为【1】

相位型SLM实现复振幅调制的方法

G与光栅频率有关，

相位型SLM实现复振幅调制的方法

这里我们以拉盖尔-高斯光（参考：光场基本模式之matlab实现（一）-拉盖尔高斯光束）束为例，则最终所使用的光栅如图：

相位型SLM实现复振幅调制的方法

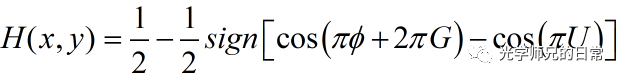
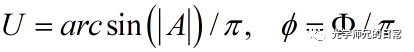
l=0,p=3

然而，实际上在对光场进行复振幅调制的过程中，这并不是唯一的方法，其它方法以后将详细介绍。

参考文献：

【1】Nape, I., Singh, K., Klug, A. et al. Revealing the invariance of vectorial structured light in complex media. Nat. Photon. 16, 538–546 (2022). https://doi.org/10.1038/s41566-022-01023-w

 

复振幅调控是光场调控中常用的手段，包括对光场振幅和相位的调控。然而，对于一般的衍射光学元件，如空间光调制器（SLM），很难直接实现对复振幅的调控。因为对于衍射光学元件来说，要么是振幅型，要么是相位型，即只能实现其中一种调控，而不能同时调控。我们在之前已经介绍过一种基于相位型SLM实现复振幅调控的方法（基于相位型SLM实现复振幅调控），但其不是唯一的。在这里我们介绍另一种方法，并基于光场传播的模拟方法对其实现的复振幅调控功能进行验证。

假设要实现调控的光场复振幅为相位型SLM实现复振幅调制的方法，则根据分析可以知道，该复振幅可以通过两个纯相位的函数叠加得到，即[1,2]

相位型SLM实现复振幅调制的方法

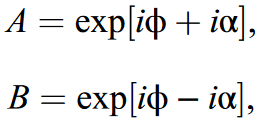
其中A和B可以通过只加载相位的方式来实现，而振幅项也变成相位的函数，有

相位型SLM实现复振幅调制的方法

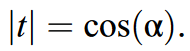
这里α和ϕ的范围都是[0,2π]。为了分别加载A和B在SLM上，采用宏像素的方法，即SLM的4个像素被当做是1个像素来用[3]

相位型SLM实现复振幅调制的方法

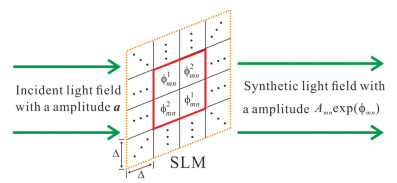
图 1 用于实现复振幅调控的宏像素[3]。

于是4个像素中处于对角位置的两个像素上分别加载相位用于调制A和B，即ϕ+α和ϕ-α，那么对于这个宏像素来说，其对入射光的调制则是A和B的叠加，而根据我们的分析又已经知道任意的复振幅光场都可以写为A和B的叠加，故仅仅需要加载相位就可以实现复振幅调控。然而需要注意，此处入射到SLM的光必须是均匀的，即没有明显的振幅起落变化。

为了验证SLM的复振幅调制效果，我们假设要通过SLM实现高阶拉盖尔-高斯光束（LG(l,p)）的调制，则此时|t|应该是高阶拉盖尔-高斯光束的振幅|LG(l,p)|，而ϕ=arg[LG(l,p)]。那么最终加载在SLM上的相位是ϕ+α和ϕ-α相间排列的结果。我们采用加载衍射光栅的方法（通过SLM产生涡旋光），其中光栅中所加载的附加相位即为ϕ+α和ϕ-α相间排列的结果，那么如果该方法是有效的，则我们可以在+1级和-1级分别得到具有相同振幅和相反相位的高阶拉盖尔-高斯光束。在此，我们基于光束传播的方法来模拟具有均匀振幅的入射光通过光栅后的衍射结果，如图

相位型SLM实现复振幅调制的方法

图 2 基于SLM的高阶拉盖尔-高斯光束（LG(l=1,p=3)）复振幅调制。

其中中间级次为零级，由于零级衍射光较强，我们对其中心区域进行了遮挡，以便+1级和-1级能够被区分，通过模拟结果可以看出，基于相位型SLM可以实现效果非常好的复振幅调控。

相位型SLM实现复振幅调制的方法

图 3 基于SLM的高阶拉盖尔-高斯光束（LG(l=5,p=10)）复振幅调制。

相位型SLM实现复振幅调制的方法

图 4 基于SLM的高阶拉盖尔-高斯光束（LG(l=5,p=10)）复振幅调制（+1级局部）。

论文信息

[1] Rosales-Guzmán, Carmelo, and Andrew Forbes. “How to shape light with spatial light modulators.” Society of Photo-Optical Instrumentation Engineers (SPIE), 2017.

[2] Takashima, Satoru, Hirokazu Kobayashi, and Katsushi Iwashita. “Integer multiplier for the orbital angular momentum of light using a circular-sector transformation.” Physical Review A 100.6 (2019): 063822.

[3] Chen, Zhaozhong, et al. “Complete shaping of optical vector beams.” Optics express 23.14 (2015): 17701-17710.

Nat. Photonics|荧光显微的原位超分辨引擎Light杰青作者优秀论文展（8） EOPC扫描振镜EOPC扫描振镜 Light杰青作者优秀论文展（6）Light杰青作者优秀论文展（6） Light杰青作者优秀论文展（4）Light杰青作者优秀论文展（4） Default Thumbnail初大平教授：更佳的3D表面测量技术，“大视场、大高差、异质材料、高精度” Interview with PIs Light杰青作者优秀论文展（7）Light杰青作者优秀论文展（7） Light杰青作者优秀论文展（3）Light杰青作者优秀论文展（3）