随机分布反馈光纤激光器辐射中极端事件的泊松分布

怪波首先是在流体力学的框架下研究的。后来，在其他科学领域也发现了相关现象。在光纤光学中，怪波的第一次观测是在超连续谱生成过程中推导出来的。此后，研究人员在不同的光纤光学实验中对光学怪波进行了研究。在此，Gorbunov等人实验研究了随机分布反馈光纤激光器辐射中出现的极端事件，重点研究它们在时间迹上的分布。研究发现，极端事件的概率取决于产生的光的波长。在光谱尾部，研究人员记录了强度比平均发电功率高50倍的极端事件。对连续波之间返回时间的分析揭示了它们的指数分布。进一步的研究发现，激光辐射中光学怪波的出现是一个随机过程，服从泊松分布，可以用特征辐射时间来表征；在所研究的激光器中，对于位于光谱边缘的振幅最大的怪波，其值从几纳秒到几十微秒不等。这一结果在光谱中心和边缘的生成中很常见，尽管它们的辐射统计数据总体上不同。此外，研究人员还揭示了遭遇截止强度概率的显著依赖律：在很宽的范围内，它符合指数为6的幂律。该工作发表在Optics letters上。

 

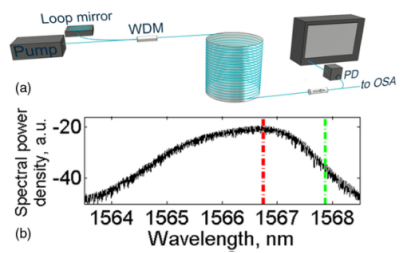
图1 (a) 实验装置。(b) 泵浦功率为3.2 W时的产生光谱。红线和绿线分别表示中心和边缘光谱滤波器的位置。

对于光谱分配，研究人员使用宽度为0.25 nm的可调谐滤波器，大致等于示波器带宽，因此，对频率平均值或代表特定光谱区域生成的真实强度的测量值没有影响。在光电探测器输入之前放置一个滤波器。测量光谱滤光片中心波长两个位置的强度-时间相关性，如图1(b)中的彩色线所示。产生的辐射在小的亚纳秒时间尺度上剧烈波动。这样，时间波动取决于它们在光谱中的位置。在中心区域，这些波动具有“一般”随机前景，最大观测强度略高于10个平均值[图2(a)]，以指数统计为特征。向光谱边缘移动会导致出现强度明显更高的孤立波，因此，它们的统计数据呈L形。在光谱的右边缘，从中心失谐1 nm，观察到强度极高的稀有波，其平均值高达50[图2(b)]。

 

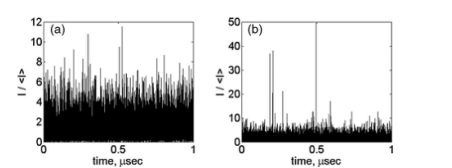
图2 在(a) 光谱中心和(b) 右侧光谱边缘测量的强度-时间动态，中心失谐1 nm。

怪波的定量定义相当随意。在海洋领域，有几种定义；最常见的是超过所谓的异常指数2。在实验中，对于光谱的中心和边缘，振幅分别高于3.56和3.67平均强度的波可以达到该值。然而，将研究局限于这些价值观是不方便的。为了进一步分析，研究人员定义了一个截止强度，所有高于该值的峰值被指定为“条件极端事件”。在这种情况下，所有研究的属性都成为截止强度的函数。

首先，跟踪中极端事件的总数显然取决于截止强度。图3给出了光谱中心和边缘的这些函数。使用的时间迹长度包括光谱中心8.107点（1 ms），边缘1.1108点（1.375 ms）。

 

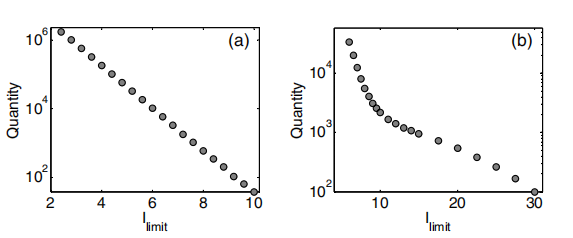
图3 对于(a) 光谱中心和(b) 光谱边缘，作为截止强度I_limit函数的强波数。

注意，给定截止强度I_limit的极端事件数除以记录道中的点总数，近似于CDF（I_limit）-累积密度函数，该函数等于极限强度概率密度函数的积分（I_limit，∞). 这些统计函数通常用inter alia来表征怪波。然而，根据定义，它们不提供有关瞬时行为值的信息。

为了分析极端事件在辐射中的分布，研究人员研究了相邻意向波对之间的返回时间-时间间隔，这是一个随机过程（图2）。最常见的方法是基于它们的值构建直方图，近似于其概率密度函数。使用存储的缓冲区构建了基于100个箱子的直方图。在从零到观察到的最大延迟的时间间隔内，已均匀地分配箱当前的截止强度。如前所述，研究人员获得了一组时间直方图，每个直方图都有其自身的截止强度值（图4）。

 

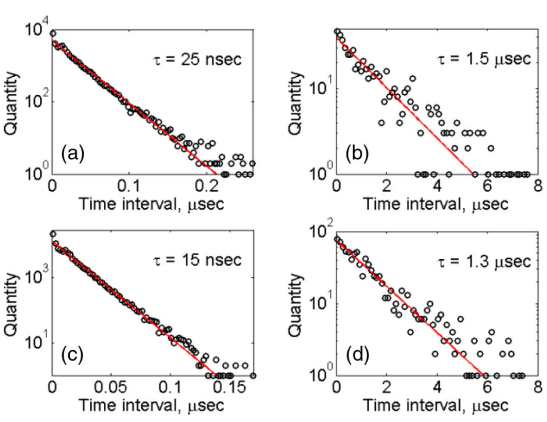
图4 极端事件之间时间间隔的直方图：实验数据（圆圈）和指数近似exp(−t/τ）（红线），截止强度I_limit等于(a) 5和(b) 8的光谱中心以及截止强度等于(c) 5和(d) 15的光谱边缘。

对于高值，缓冲区大小较小，难以识别曲线形状；然而，很可能所有大于4<I>的直方图都遵循指数定律exp(−t/τ）。注意，这些值都符合怪波的通用定义。更有趣的是，尽管总体极值统计数据存在巨大差异，但该特征对于滤波器的两个光谱位置都是通用的（图3）。特征辐射时间对于光谱的中心和边缘是不同的且取决于截止强度值。对于光谱的中心部分，特征辐射时间的变化范围从小截止强度值的数百皮秒到截止强度为10的约20微秒。在光谱边缘，截止强度为30的特征时间从几纳秒到15微秒不等。对于更大的截止强度，特征辐射时间趋于接近数百微秒，但可用的直方图缓冲区不够大，无法进行实体近似。中心和边缘的一般特征辐射时间值都是几十到几百纳秒，即10³纳秒−比强烈波的宽度大10⁴倍。

众所周知，后续随机事件之间时间延迟的指数分布是泊松分布的特征，泊松分布描述了在一个时间单位内随机事件发生概率固定的过程。因此，FL-RDF辐射中的极端事件根据泊松定律出现的假设是令人信服的。为了证明这一点，我们提供了以下数学验证。关于遇到n个随机事件的概率ωn的知识允许计算遇到具有随机事件的EE的概率，在一次测量中，振幅高于截止强度。实际上，在时间间隔发生的随机事件的平均数量由n=t/τ(I_limit)给出。由于τ根据固定极限强度下的时间间隔直方图计算，它是截止强度的函数，可直接指示。同时，在该时间间隔内测量的总数为N(t)=t/δt，其中，δt为离散化间隔。因此，概率由n和n(t)之间的比率给出：CDF(I_limit)=δt/τ(I_limit)。另一方面，CDF可以通过选择截止强度值的强波总数来估算（图3）：N(I_limit)=N(t)·CDF(I_limit)。将后两个表达式中的CDF(I_limit)等效，得到特征辐射时间与轨迹中极端事件数量之间的关系。因此，将跨时间间隔的更一般分布推导出不太一般的分布。

图5(b)中绘制的曲线很有趣，不仅因为它的长翅膀，而且它的中心部分似乎非常精确地服从幂律。在图6中，强波在时间单位内被包围的概率用幂律拟合，为了更好地显示，研究人员将 x 轴上的步长减少到0.1平均强度。α = 6.049，非常接近6的整数。注意，幂定律对于强度是不常见的，在随机辐射的情况下，应该在这里解释指数相关性。

 

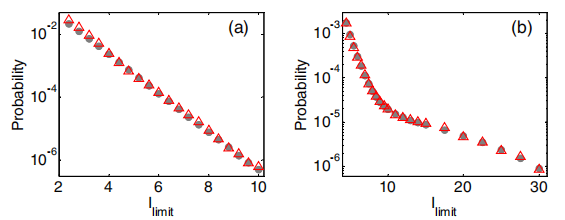
图5 CDF（圆圈）和时间单位δT/τ（三角形）中的无量纲辐射概率作为截止强度I_limit值的函数。(a) 光谱中心和(b) 光谱边缘。

 

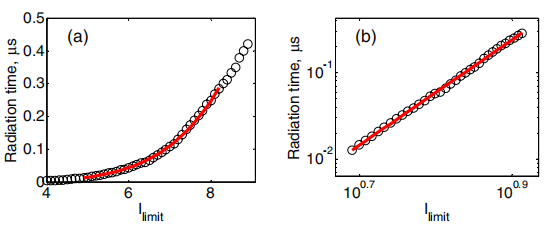
图6  作为截止强度函数的辐射时间（圆圈）及其幂函数近似值（红线）。

综上所述，研究人员研究了在随机分布反馈光纤激光器中出现的极端事件的分布。研究表明，在光谱边缘，存在振幅高达平均功率50倍的单一强度波而在光谱中心，强度概率密度函数接近指数。分析表明，相邻极端事件对之间的时间间隔代表一个服从指数分布的随机值。这种分布对于泊松过程来说是独特的且可以通过单值特征辐射时间来表征。假设怪波的产生是一个泊松过程，研究人员建立了特征辐射时间和遇到的波数之间的解析关系。