神经网络实现光学涡旋模式的宽带高效识别
专家视点
目前,人们开发了各种方法来产生具有中心相位奇点的光束,例如,拉盖尔-高斯光束,高阶贝塞尔-高斯光束,高阶马蒂厄光束和甜甜圈空心光束。在此,茅志翔等人提出并实现了一种混合涡旋光束,通过使用基于改进的Alexnet结构的卷积神经网络模型来实现高效的单模轨道角动量信息传输系统,携带轨道角动量的混合光束为识别光的轨道角动量提供了更可控的自由度。具体地,研究人员给出了训练样本分辨率(或与精度相关的数量)与模型训练时间之间的关系。此外,研究人员还研究了以下三个重要参数对混合涡旋束的轨道角动量识别精度的影响:混合束的拓扑荷l、角比n和传播距离z。实验中,这些轨道角动量模式的分辨率可以精确区分为0.01(n)。当轨道角动量l为1-10,n为0.02-0.99时,不同轨道角动量模式的识别准确率接近100%。因此,n的宽可调范围显示了光通信中轨道角动量模式的产生和检测的宽带宽。该工作发表在Physical Review Applied上。

Zhi-Xiang Mao, Hai-Yu Yu, Meng Xia, Sheng-Zhe Pan, Di Wu, Ya-Ling Yin, Yong Xia, and Jian-Ping Yin, Broad bandwidth and highly efficient recognition of optical vortex modes achieved by the neural-neTWork approach, Physical Review Applied, 13(3): 034063 (2020).
目前,人们开发了各种方法来产生具有中心相位奇异性的光束,例如,拉盖尔高斯光束、高阶贝塞尔高斯光束、高阶马蒂厄光束和环形空心光束。除了用于生成结构光的线性过程之外,非线性过程也可以用于生成结构光。这样的激光束具有独特的物理特性,例如,携带桶形强度分布、螺旋波前、中心相位奇异性和暗中心强度且它们还可以携带自旋和轨道角动量并表现出空间传播不变性。最近,由于可获得的轨道角动量模式的无限范围,光的轨道角动能已被用于实现光载波数据承载能力的复用。正因为如此,人们发现轨道角动量在量子信息处理和光通信中有许多应用。例如,基于轨道角动量的自由空间光通信被认为是下一代通信领域的一个很有前途的应用,它可以克服目前受到大量数据、云计算和人工智能限制的通信速度和容量限制。
帕吉特及其同事于2004年开创了基于轨道角动量的自由空间光学通信的先河。在他们的实验中,全息图被用来将轨道角动量激光器分裂成九个独立的螺旋,然后通过空气传播15米到达接收望远镜,因此,所有模式都被区分并同时读出。此外,在基于轨道角动量的光通信方面,接收器识别轨道角动量模式的能力对于轨道角动量分割复用也是至关重要的。事实上,轨道角动量束的检测可以使用多种技术进行,包括全息光栅、干涉仪、模式转换器和变换等。所有这些方法都为有效的基于轨道角动量的光通信铺平了道路。
另一方面,机器学习在图像识别中具有高精度,其中大量图像被用作训练集,使得机器可以随后处理和表征新数据。最近,机器学习在图像分类、语音识别、光通信等领域引起了相当大的关注。目前,有几种机器学习模型被证明可以解决实验中出现的轨道角动量识别问题,如人工神经网络、深度神经网络和卷积神经网络。此外,研究人员还提出并研究了几种理论方案,包括K最近邻、支持向量机和朴素贝叶斯分类器。为了提高识别的准确性,研究人员研究了结构更复杂的卷积神经网络模型。Lohani和Glasser设计了一个基于定制卷积神经网络的网络,该网络具有单层卷积和池。Tian及其同事提出了一种轨道角动量偏移键控自由空间光通信系统,该系统具有卷积神经网络的六层卷积和池化层。Doster和Watnik使用AlexNet结构的经过训练的卷积神经网络作为分类器,该网络具有五个卷积层、三个池化层和三个完全连接的层,以区分携带轨道角动量的多重贝塞尔-高斯光束。更具体地说,携带不同轨道角动量状态的拉盖尔-高斯和贝塞尔-高斯光束用作多路传输信息流的通道。卷积神经网络模型识别轨道角动量的大多数方法都给出了轨道角动量模式传输的±l叠加,这将两个轨道角动量模型叠加在一起,符号相同但相反,以传输信息或复用轨道角动量模式。另一种方法是复用更多的轨道角动量模式来传输信息。两种轨道角动量模式叠加方案获得的光强分布具有复杂的花瓣形状,其显著特征适合于图像的进一步识别。然而,单模轨道角动量传输通信通常被认为不适用于自由空间光通信;这是因为其“甜甜圈”类型的强度分布或其光束大小不具有定量识别特征,导致识别精度低。
01
设计与方法
图1显示了产生轨道角动量束的实验装置。高斯光束从高度稳定的氦氖(HeNe)激光器(HRS015B,Thorlabs)入射。中心波长为632.991nm的稳定HeNe激光器提供了强度稳定。激光器具有高质量的输出模式,其输出功率恒定,精度小于0.3%。物镜、光阑孔径和共焦透镜用于准直光束并去除任何其他高阶衍射项。然后,光束穿过半波片,该半波片改变光束的偏振方向以满足空间光调制器的要求。接下来,分束器(BS)将光束分为两部分,其中一部分可以被反射并转化为携带轨道角动量的混合光束。在实验中,空间光调制器(holoeye)是一种仅相位反射的液晶器件,分辨率为1920 × 1080像素和8.0 µm像素间距。最后,可以在CCD相机上观察到轨道角动量束。此外,z表示空间光调制器和CCD之间的距离。
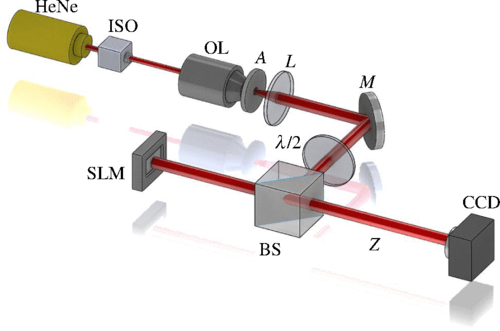
图1 生成轨道角动量光束的实验装置。HeNe:HeNe激光源;ISO:光学隔离器;OL:物镜;A:孔径;L:透镜; M:镜子;λ/2:半波板;BS:分束器;SLM:空间光调制器;CCD:电荷耦合器件;Z:空间光调制器与CCD之间的距离。
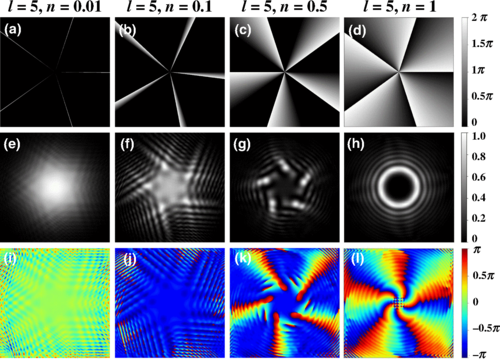
图2(a)(e)(i) 相应地表示 l=5 加上 n=0.01 的 轨道角动量光束的螺旋相位分布、归一化光学强度分布和相位分布。(b)(f)(j)表示 l=5加上n=0.1的轨道角动量光束的相应三个分布。(c)(g)(k)表示 l=5 加上n=0.5 的轨道角动量光束的相应三个分布。(d)(h)(l)表示轨道角动量的相应三个分布,其中,l=5 加上 n=1。相位和强度颜色条显示在图的右侧,其中,强度条被归一化。
研究人员得到这些轨道角动量光束的计算全息图和强度分布,如图3所示。以l =3为例,分别给出了n=为0.01、0.5、0.9和1.0的全息图。然后,研究人员在理论和实验中分别给出了l=1、3、5和n=0.01、0.5、0.9、1.0的轨道角动量光束的强度分布。实验结果与理论实验基本一致。从图3中可以看出,当n接近0时,轨道角动量光束退化为一个具有微小相位调制的高斯光束。当n接近于1时,光束实际上将成为传统的轨道角动量光束。在这两种情况下,从强度分布中揭示出的轨道角动量信息都很少。然而,在0<n<1时,光束开始以花瓣或条纹的形式显示轨道角动量信息,这是神经网络对轨道角动量信息的实际表现形式。
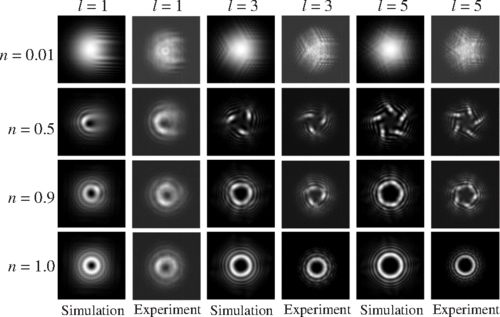
图3 在第一列和第六列中,在理论和实验中,分别用l=1、3、5和n=0.01、0.5、0.9和1.0绘制了轨道角动量光束的强度曲线。
图4显示了n对混合光束总轨道角动量影响的模拟结果。可以看出,随着参数n的变化,光束的总轨道角动量在一个固定的l条件下保持不变。光束的总轨道角动量与设计的各种轨道角动量的量子数l一致,表明高斯光束携带零个轨道角动量,混合光束携带l个轨道角动量。即高斯光束的引入对总轨道角动量的值没有影响,这意味着可以改变轨道角动量光束的强度分布并保持总轨道角动量不变。对于一个给定的l,只要n的值在0-1的范围内,轨道角动量光束的l在光束的传播过程中就不会发生变化。这一令人印象深刻的特性意味着角比将为光通信系统提供更多可控的轨道角动量自由度。当传输相同的轨道角动量信息时,只要n在0-1的范围内,不同的传输端就可以发送不同的花瓣图案。因此,该方法将大大提高轨道角动量传输的带宽。
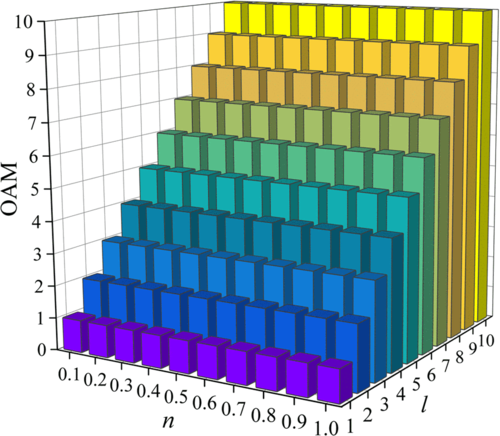
图4 混合光束的总轨道角动量作为n, l的函数是所设计的轨道角动量的量子数,它等于总轨道角动量。
单模轨道角动量波束传输系统,如图5(a)所示。激光源输出腰部为1.2 毫米的高斯激光束。然后,研究人员将光束入射到加载到空间光调制器上的相位模板上,空间光调制器使用不同的计算全息图进行编程,用于将高斯光束调制到相应的轨道角动量光束中。接下来,轨道角动量光束在自由空间中传播。最后,通过CCD相机获取光束的强度图像。这种方法基于卷积神经网络,在这里用于识别检测到的轨道角动量波束序列的轨道角动量。通过在空间光调制器上加载不同的全息图,研究人员收集大量相应的强度曲线来训练我们的神经网络模型,使用不同的参数I,n和z(I=1,2,3,...,10;n=0.01,0.02,...,1和z=21,22,...,50 厘米)。卷积神经网络的一般结构,如图5(b)所示。研究人员使用分辨率为256×256像素的电荷耦合器件图像作为输入并使用l=1,2,3,...,10的概率作为输出。
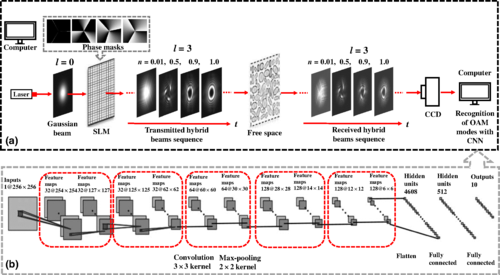
图5 (a)轨道角动量传输系统的结构图。(b)基于我们设计的卷积神经网络的轨道角动量识别方法的结构图。
研究人员使用了一个优化的卷积神经网络模型,它在AlexNet结构上得到了完善,培训采用了Keras框架。研究人员所利用的改进网络称为AlexNet,由5个卷积层和3个全连接层组成,如图4(b)所示。该网络中的变体包含了大约260万个可训练的权值。如表I所示,研究人员构建了包含三个子层的Conv1层,它们在图5(b).中用红色虚线圈起来第一个子层是一个二维卷积层,组织有32个特征映射。第二个子层是批量归一化层,它帮助神经网络克服梯度消失或梯度爆炸。最后一个子层是最大池化采样层。如所述,最大池化层可以降低表示的维数,从而产生对小偏移和失真的不变性。
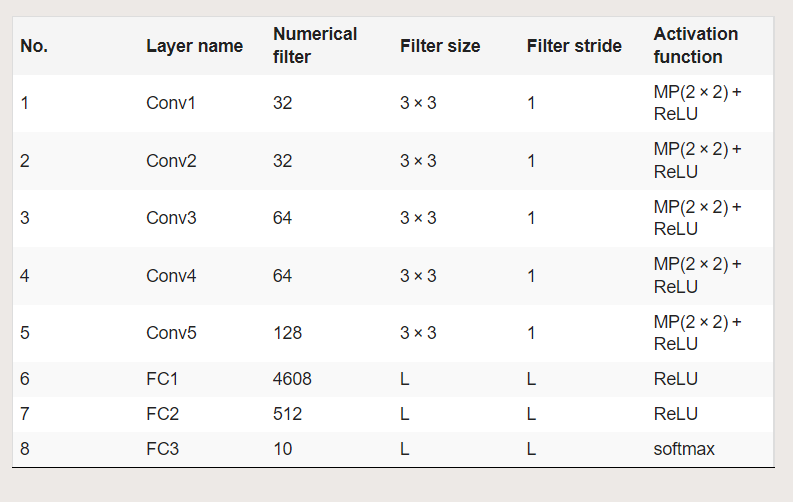
表1 卷积神经网络模型的体系结构。
Conv2 层到 Conv5 层的结构与 Conv1 层的结构相似,只是特征图的数量不同,如表1所示。重复此结构单元五次的主要目的是识别更多的轨道角动量值。在二维卷积层、MP层和全连接层中,选择整流线性单元作为非线性激活函数,因为它的收敛速度比传统的非线性函数更快。最后,输出进入最后一个完全连接层,使用Softmax作为激活函数。该层的输出是检测到的轨道角动量光束的模式。
首先,在实际模型训练过程中,具有不同参数(I=1,2,3,...,10;n=0.01, 0.02, ...,1.00和z=21,22,...,50 cm) 累积并划分为训练集和测试集(训练为 80%,测试为 20%)。然后,研究人员对所有数据进行预处理并将图像剪切并缩放到以光轴为中心的256×256像素。如图6(a)所示,以I=4为例,每个强度曲线将顺时针或逆时针旋转最多15°,切割多达10%的边缘,放大多达20%并移动高达10%的水平和垂直方向。卷积神经网络训练参数如下:迭代次数=50,批量大小=10。例如,训练集的损失和精度变化,如图6(b)所示。黑线是精度的变化,红线是损失的变化,实线代表训练集,虚线代表验证集。这表明,数据预处理可以保证所生成模型在实验过程中一些物理偏差的稳定性。epochs = 50 时,迭代次数足以使模型的损失函数收敛,表明模型训练是成功的。
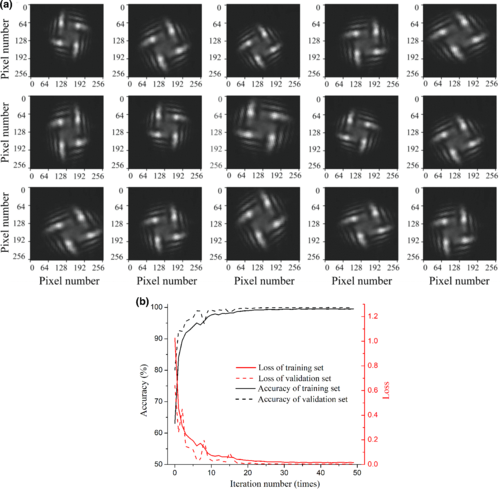
图6 (a)以l = 4为例,用于训练和验证卷积神经网络的混合波束的子集。给出了模拟光束的半径、质心和轨道角动量光束方向的一定值。(b)当迭代次数达到50次时,损失函数和精度达到收敛。
02
神经网络用于识别光学涡旋模式
由于样本分辨率对轨道角动量识别精度的影响,研究人员首先研究了训练样本图片的分辨率对轨道角动量识别模型的准确性和训练时间的影响。研究人员随机选择大约 4000 个轨道角动量光束强度剖面作为训练样本,将其分辨率修改为从20×20像素到 256×256像素的一系列不同值并单独训练每个模型。最终获得的稳定精度和训练时间绘制在图7(a)中。因此,低分辨率的样品的精度非常低,但随着分辨率的提高而迅速增加且在约50×50像素时趋于饱和。随着像素数的增加,精度趋向于一个值为98.7%的常数。其次,模型训练的时间随着分辨率的增加而线性增加。此外,由于图形处理器视频内存大小的限制,无法得到超高分辨率样本,需要在系统的计算复杂性和识别效率之间做出权衡。因此,研究人员选择50×50像素的分辨率作为模型的输入大小。这允许98.03%的高精度和11分钟的短训练时间。
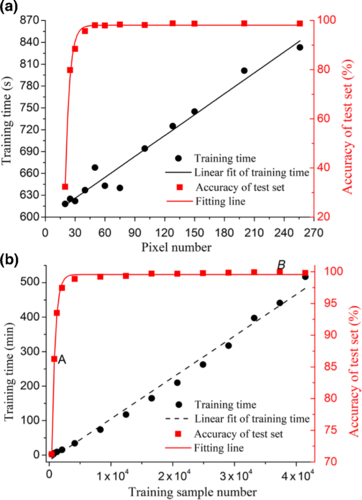
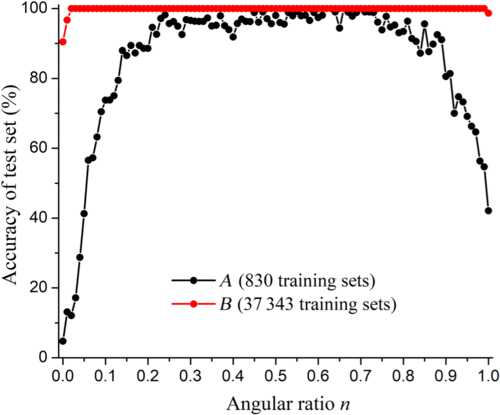
图7 基于卷积神经网络方法识别10种轨道角动量模式(l=1、2、3、...,10)的性能。识别10个单一轨道角动量模式的准确性和训练时间作为像素(a)和训练样本(b).的函数为了简化描述,在(a).的水平纵坐标中使用了一维像素在(b)中,在A点,训练编号为830;在B点,训练编号为37343。
为了探究样本数对轨道角动量识别精度的影响,研究人员还研究了训练样本数对模型的精度和训练时间的影响。根据之前的研究和实验条件,研究人员选择了256×256像素的分辨率作为样本图像的分辨率。研究人员随机选择一系列有多达40000个样本的集合作为训练样本并分别训练每个模型。最终得到的稳定精度和训练时间如图7(b)所示。从图7中可以看出,这些结论与上述分辨率研究的结果相似。低样本的精度较低,但随着样本数量的增加迅速增加并在4000左右接近饱和,仅为4000,远不是40000的总数。随着训练样本数的增加,准确率趋于不变,其值为99.93%。将图7(b)中的A点与B点进行比较,随着训练集数量的增加,轨道角动量识别的精度显著提高。注意,模型训练的时间随着训练样本数量的增加而呈线性增加,仍然需要在系统的计算复杂性和识别效率之间进行权衡。因此,研究人员选择40000个作为训练样本的总数,准确率为99.93%,训练时间为517 分钟。
参数l、n、z对轨道角动量识别精度的影响。首先,l表示轨道角动量光束的拓扑荷数,n表示螺旋相在混合相上的角比,z表示空间光调制器与电荷耦合器件之间的距离。由于使用了不同值的强度轮廓图像(l = 1、2、3、...,10;n = 0.01、0.02、...,1.00和z = 21、22、...,50 cm),因此,在训练模型时,研究人员还研究了l、n和z对最终模型精度的影响。研究人员在图7(b)中选择了两个训练样本A和B作为观察点。点A表示由830个训练集训练出来的模型,在测试集上的平均准确率为86.24%。点B代表了37 343个训练集的模型,在测试集上的平均准确率为99.93%。如图8(a)所示,研究人员研究了z对轨道角动量识别精度的影响。黑色方块表示模型A中不同z的测试样本的精度,红色方块表示b点处不同l的测试样本的精度,红线、黑线为拟合线。研究表明,在训练样本较少的情况下,模型精度随z的增加而略有降低。然而,在进行了大量培训的情况下,模型的精度不受z的影响。
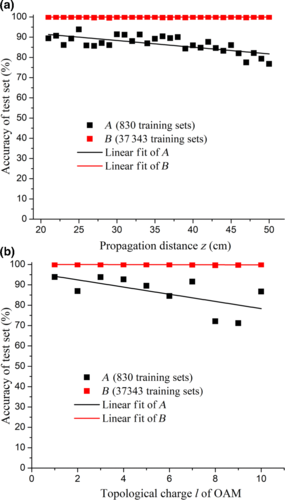
图8 轨道角动量的(a)中的传播距离z和(b)中的拓扑荷l对轨道角动量识别精度的影响。黑色方块表示A点测试样本的精度,红色方块表示B点测试样本的精度。红线和黑线呈线性拟合。
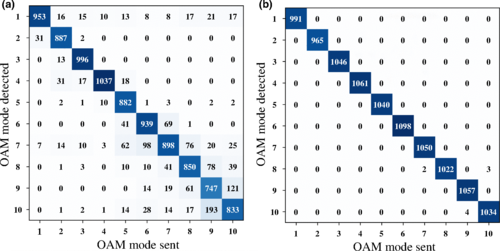
如图8(b)所示,研究人员研究了拓扑荷数l对轨道角动量识别精度的影响。在实验中,总共测量了l = 1、2、3、...,10。当训练样本较少时,精度随着l的增加而降低。主要原因是拓扑荷数越大,模型需要识别的轨道角动量光束的特征细节就越多,识别的误差也就越多。当然,当样本数量足够时,在B点的模型识别精度非常高,接近100%。图9显示了不同l的混淆矩阵,可以用来进一步描述发送的轨道角动量模式和检测到的轨道角动量模式的分布。从图9中可以看出,误差样本分布在真实的l附近。获以及精密光谱学领域的进展。
最后,研究人员研究了n对l=1-10和距离z=21-50 cm时轨道角动量光束轨道角动量识别精度的影响,如图10所示。对于小训练样本,当n<0.2或>0.8时,准确率下降幅度较大;n为0.2-0.8时,精度大于90%;当n<0.2时,轨道角动量光束的强度分布接近高斯光束,如图3所示,导致轨道角动量信息的细节反射较少并产生低精度。当n大于0.8时,强度曲线接近“甜甜圈”曲线,如图3所示,并且能够反映轨道角动量信息的轮廓也非常有限,这也会导致精度降低。对于大量训练样本(B为37,343个训练集),当n为0.02-0.99 时,准确率接近100%。随着训练集数量的增加,轨道角动量 识别的准确性显著提高。当l 的范围从1到10,并且n为0.02-0.99 时,轨道角动量的识别准确率接近 100%,n 的最小间隔为0.01。这意味着基于混合相结构的轨道角动量生成和检测的带宽很宽。卷积神经网络模型以前从未见过测试集中的每个轨道角动量模式,但随着样本数量的增加,它仍然能够识别整个轨道角动量模式并突出显示模型的稳健性。
在图像识别问题中,最重要的因素是稳定、可靠和量化的识别特征,例如,条纹、点或狭缝的数量。在大多数研究中,携带不同轨道角动量状态的拉盖尔-高斯和塞尔-高斯波束充当多路复用信息流的通道。但是,“甜甜圈”强度曲线用于通过机器学习来识别轨道角动量,但准确性并不高。这样做的原因是,它们依赖于“甜甜圈”强度分布的大小和宽度,而不是监督学习的特定特征和量化特征。当一些外部干扰因素被添加到整个数据集中时,例如,预处理缩放和传播距离发生变化,“甜甜圈”的大小和宽度也会随着这些因素而变化。在一般的实验中,各种角动量模态叠加形成的干涉图案具有识别轨道角动量的非常明显的特征。与多路复用多个轨道角动量模式相比,单模轨道角动量信息传输系统的实验方案更加简洁。研究人员使用的混合光束可以提供轨道角动量的更多自由度,包括拓扑荷数和角比 。花瓣干涉图案的数量和形状可以为轨道角动量识别携带更多的信息且还保证了轨道角动量识别的高精度以及优化的卷积神经网络模型。
总之,研究人员利用卷积神经网络模型实现了轨道角动量模式的宽带宽和高精度识别。混合波束承载轨道角动量用于为轨道角动量模式的识别提供更可控的自由度。在实验中,精确区分了间隔小至角比0.01的不同轨道角动量模式。当轨道角动量的量子数范围为1-10,角比从0.02到0.99时,不同轨道角动量模式的识别准确率接近100%。因此,角度比的宽可调范围对应于轨道角动量模式的生成和检测的宽带宽。研究表明,光束强度分布中固有的稳定、可靠和量化的识别特征对于轨道角动量识别问题至关重要。与多路复用多个轨道角动量模式相比,单模轨道角动量信息传输系统的实验方案更加简洁。在实验中,考虑了拓扑荷为整数的轨道角动量模式。最近,具有分数拓扑荷的轨道角动量模式也可以通过深度学习方法精确识别。这个方案表明,下一代基于卷积神经网络的轨道角动量光通信具有广泛的通用适用性潜力。这个方案可以扩展到更广义的光束,叠加两个或多个拓扑荷。多种轨道角动量模式叠加形成的干涉图样,对识别轨道角动量也有非常明显的特征。光强度分布的花瓣图案确保了机器学习识别的高精度。此外,角比的广泛可调范围相当于轨道角动量模式的生成和检测的宽带宽。结果与单模方案的结果相似;然而,更多的轨道角动量模式的传输通信可以提高光通信中的信息容量。

研究人员简介

夏勇,华东师范大学物理与电子科学学院精密光谱科学与技术国家重点实验室教授,研究方向为MgF分子激光冷却与囚禁、人工智能与结构光场。
E-mail: yxia@phy.ecnu.edu.cn
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。