强场电离探测强涡旋脉冲的轨道角动量
随着飞秒激光的发展,光学涡旋的产生和应用已经扩展到强光与物质相互作用的领域。强涡旋脉冲轨道角动量的表征是非常关键的。在此,方一奇等人提出并实现了一种新的基于光电子的方案,可以在不改变光螺旋相位的情况下原位区分聚焦的强飞秒光学涡旋的轨道角动量。在实验中,电离速率是在每个激光脉冲电离不到一个原子的条件下控制的。在这种强烈的激光脉冲中,有大量的光子(>1015),氩原子的多光子电离只吸收了大约10个光子,因此,测量过程对涡旋脉冲的轨道角动量状态几乎没有影响。在光学上,研究人员在强场光电离实验中使用了双色共旋转强圆形场,其中一个色光场是作为探测脉冲的平面波,另一个是需要表征其轨道角动量的涡旋脉冲。研究表明,通过控制探测脉冲的空间分布,可以通过测量相应的光电子动量分布或角度分辨产率来清楚地识别涡旋脉冲的轨道角动量。这项工作为涡旋光脉冲提供了一种新的原位探测场景,并对研究具有光学轨道角动量的超快和强复杂光场具有意义。该工作发表在Light: science & applications上。

Yi-Qi Fang, Zhen-Ning Guo, Pei-Pei Ge, Yan-Kun Dou, Yong-Kai Deng, Qi-Huang Gong and Yun-Quan Liu, Probing the orbital angular momentum of intense vortex pulses with strong-field ionization, Light: Science & Applications 11: 34(2022).
光学涡旋光束携带众所周知的光学轨道角动量。光学轨道角动量为现代科学的各个领域提供了非常重要的自由度,如粒子光镊、量子通信、电信、天体物理学、显微镜和生物学。由于涡旋光束的动力学特征由轨道角动量模式(或拓扑荷)决定,因此,轨道角动量模测量是涡旋光束应用之前的关键任务之一。迄今为止,轨道角动量检测方案大多是通过光学方法实现的。一种主要方法是利用干涉技术,其中特定干涉图中的条纹数量与拓扑荷有关。另一种传统的选择是使用具有特定掩模的衍射图案,例如,三角孔径衍射、环形孔径衍射和线性或角狭缝衍射。此外,一些方法,如共形映射、多平面光转换、鲁棒模式转换器、旋转多普勒效应和二维材料,也显示出测量涡旋光束轨道角动量的能力。
几乎所有这些传统的光学方法都可以被视为强耦合检测且测量本身不可避免地会修改光束的轨道角动量状态。为了克服这一问题,最近,光学轨道角动量的弱测量在理论和实验上都得到了证明。弱测量通常包括三个阶段:待测系统在初始状态下准备;则系统与探针弱相互作用;最后,对系统的最终状态进行后选择。然而,对于复杂的弱测量方法,光子轨道角动量的无损检测也很难实现。因此,有必要寻求替代和直接的方法来探测光的轨道角动量状态而不发生轨道角动量态坍缩,以便随后可以在后续应用中使用所测量的光学涡旋光束。
在强场领域,得益于超快激光的快速发展,飞秒涡旋脉冲在强光-物质相互作用研究中引起了越来越多的关注。如今,涡旋脉冲已被用于极紫外区域拓扑场的超快时空操纵,例如,产生具有时变轨道角动量的极紫外光束并同时控制阿秒脉冲的自旋-轨道动量。强的涡旋脉冲也产生了光电离或光激发过程的新选择规则,伴随着独特的角动量跃迁。最近,通过光电离实验,研究人员相继证明了光学聚焦系统中轨道角动量相关的二向色光电效应和强光场的自旋-轨道耦合。在强场条件下,强激光脉冲和目标之间的相互作用通常在高真空环境中进行,光脉冲必须聚焦到小空间尺度以获得高强度且高集中的激光能量对光学仪器具有破坏性。这些障碍阻碍了传统光学方法在原位探测强场涡流脉冲的轨道角动量方面的适用性。到目前为止,在那些强的光-物质相互作用过程中,光轨道角动量的测量和应用研究较少。
01
研究人员在图1a、b中说明了实验方案。激光脉冲(800 nm,25 fs)工作在3 kHz。通过与250 μm厚的β-硼酸钡晶体倍频产生二次谐波(400 nm)。在实验中,研究人员使用800 nm光场作为探测脉冲,而400 nm光场的轨道角动量需要表征为未知脉冲。探测脉冲和未知脉冲分别由马赫-曾德尔干涉仪方案控制。在探测脉冲臂中,可以选择使用自制的2毫米水平狭缝来雕刻光束的空间轮廓。在未知脉冲臂中,利用光阑孔径来控制聚焦时未知脉冲的空间尺度。研究人员使用螺旋相位板将光转换成涡旋脉冲。在这里,准备了具有三种不同轨道角动量模式的未知光束(ℓ = 0、1和2)。在实验中,探测脉冲和未知脉冲的光束半径被控制为~9 mm和~4.5 mm。如图1c所示,探测脉冲和未知脉冲的偏振都被调整为右圆偏振,它们的合成激光场被称为双色共旋转圆激光场。探测光束和未知光束之间的相对时间延迟由一对熔石英楔进行微调,精度约为0.004π rad(~5 阿秒)。
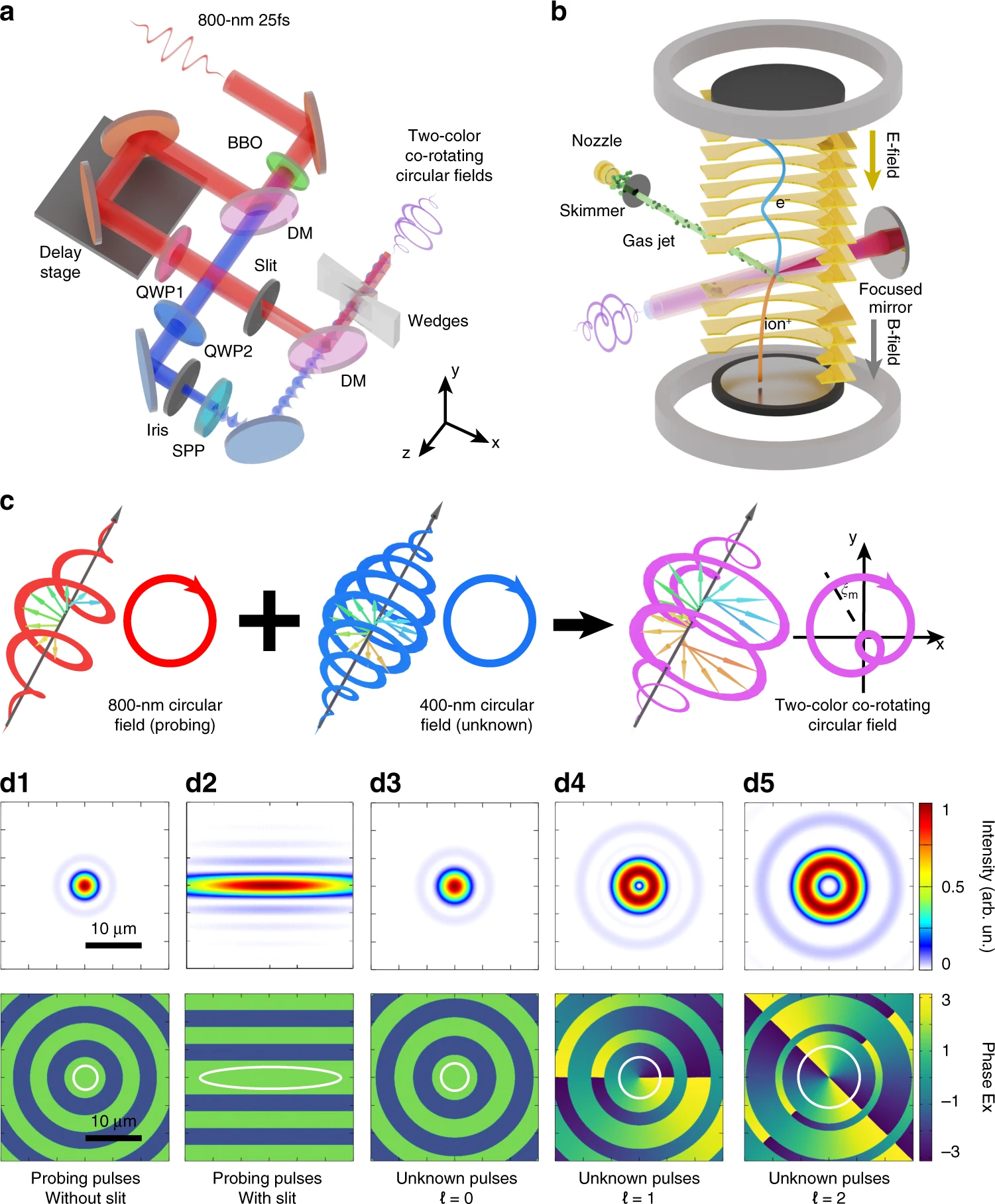
然后,如图1b所示,研究人员通过75 mm焦距镜(数值孔径 为 0.17)进入高真空室(5 × 10−11 mbar)。在激光-原子相互作用区域,探测脉冲和未知脉冲的峰值强度被校准为Ipr = 5.6 × 1013 W cm−2和Iun = 3.5 × 1012 W cm−2。在焦点处,合成场与超音速氩原子气体射流相互作用。产生的光电子由带有位置敏感探测器的飞行时间光谱仪测量,然后构建其三维光电子动量分布。
为了分析焦平面中双色光场的几何结构,研究人员使用Richards–Wolf矢量衍射方法模拟光场的空间分布。在图1d中,给出了x分量电场强度和相位的计算分布。探测脉冲的强度显示为焦平面中的类高斯分布(图1d1)。注意,当在光路中添加2 mm水平狭缝时,焦点处探测脉冲的强度分布水平拉伸(图1d2)。这里,将不带狭缝的探测脉冲(图1d1)和带狭缝的(图1d2)分别称为非空间雕刻探测脉冲和空间雕刻探测信号。另一方面,未知脉冲的空间大小与轨道角动量值有关(图1d3-d5)。激光强度的焦点分布表现为典型的环形结构(图1d4,1d5)。模拟结果表明,在焦平面中,未知脉冲点(图1d3-d5)大于非空间雕刻探测脉冲点(图1d1)。这种光配置导致一个重要的结果,即空间雕刻的探测脉冲的水平尺寸远大于未知脉冲的光点,但同时,其垂直尺寸小于探测脉冲。如稍后所示,这将允许人们在实验上巧妙地探测未知脉冲的拓扑相位结构。
首先,研究人员使用非空间雕刻探测光场(图1d1)探测未知脉冲的轨道角动量(图1d3-d5)。通过在实验中固定楔形物的位置,稳定了双色场的相对时间延迟。然后,通过在双色激光场中使用不同拓扑荷的未知脉冲来测量光电子动量分布。可以观察到,当ℓ为零,光电子动量分布显示为典型的新月形波瓣(图2a)。相反,当ℓ 非零时,光电子动量分布表现为完美的环形结构(图2b,c)。
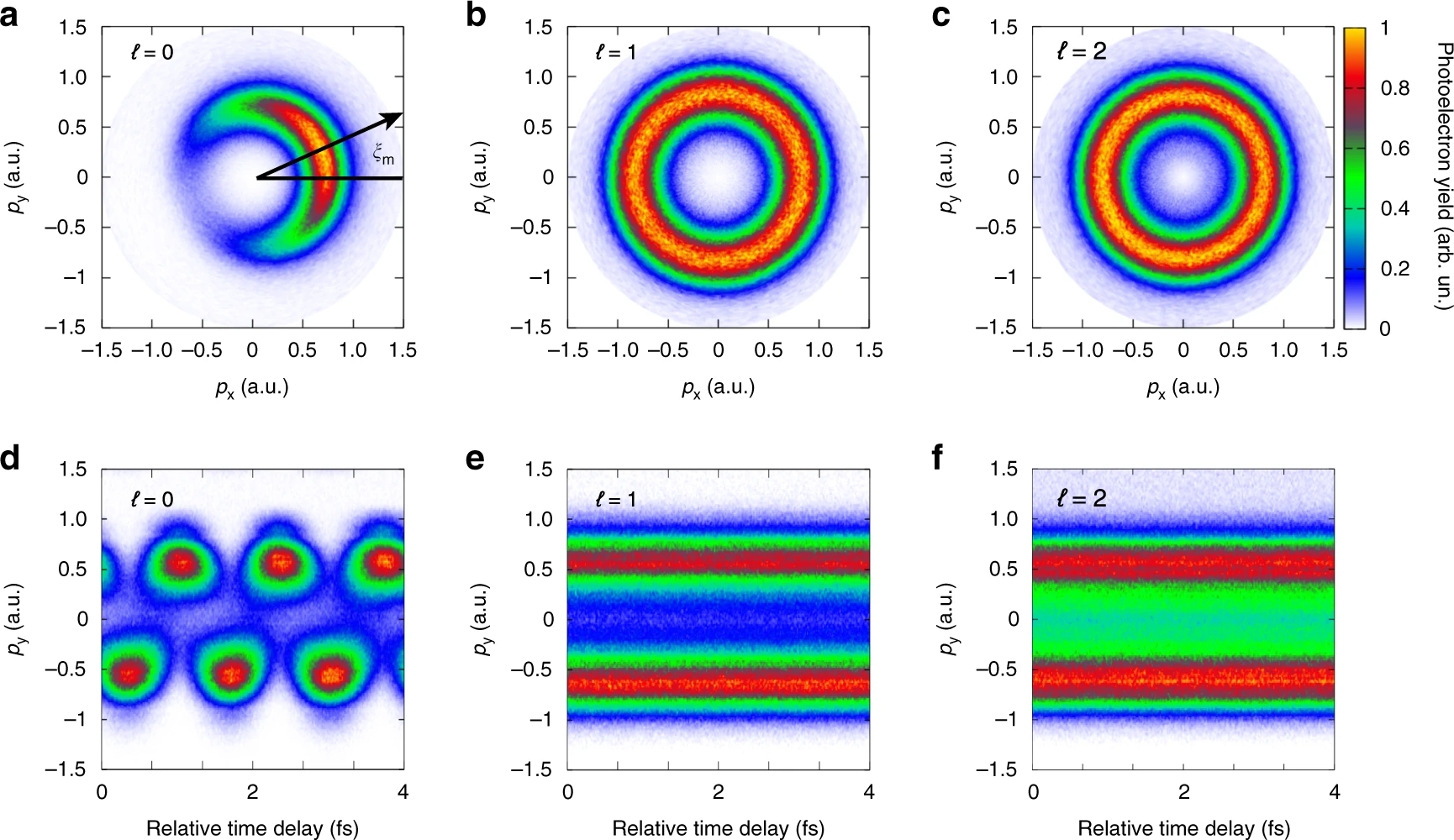
这种突出的现象与合成双色场的相对相位Δϕ有内在的联系。在时域中,由共旋转电场矢量的尖端绘制的李萨如曲线在每个激光周期中具有单个最大值。在周期性电场中,电离的光电子达到这个最大值,在电子动量分布中形成峰值,形成月牙形的波瓣。应注意,月牙形瓣的偏转角ξm与相对相位Δ。关系式可由ξm = −Δϕ 给出。这里,相对相位由相对时间延迟Δt和双色场的空间相位结构决定,即Δϕ = ωunΔt + ℓφ,其中ωun是未知脉冲的角频率,φ = tan−1(y/x)是焦平面中的方位角。由于光电离可以发生在焦光点的任何点,因此,“探测器”上测量的光电子动量分布是整个焦平面产生的光电子信号的叠加。当未知脉冲轨道角动量为零时,双色场的相对相位在空间上是均匀的。从焦点中不同位置电离的光电子具有相同偏转角的光电子动量分布,因此,在图2d中显示了典型的新月形波瓣。
当未知场具有非零轨道角动量时,双色场的相对相位分布在焦平面上是不均匀的(图3a, b),这与ℓ= 0的情况不同。研究人员利用ammosov-delon-krainov理论计算了局域光离率分布并圈定了光离率W(x,y)大于0.05 Wm(Wm为焦平面内最大局域光离率)的主导区域(图3虚线圈)。如图3a, b所示,在这个优势区域内,双色场的相对相位是方位相关的。从焦平面不同方位释放的光电子形成了不同偏转角的光电子动量分布。这些偏转角的范围为0到2πℓ,因此,测量到的“探测器”上的光电子动量分布显示为一个环空(图2b, c)。
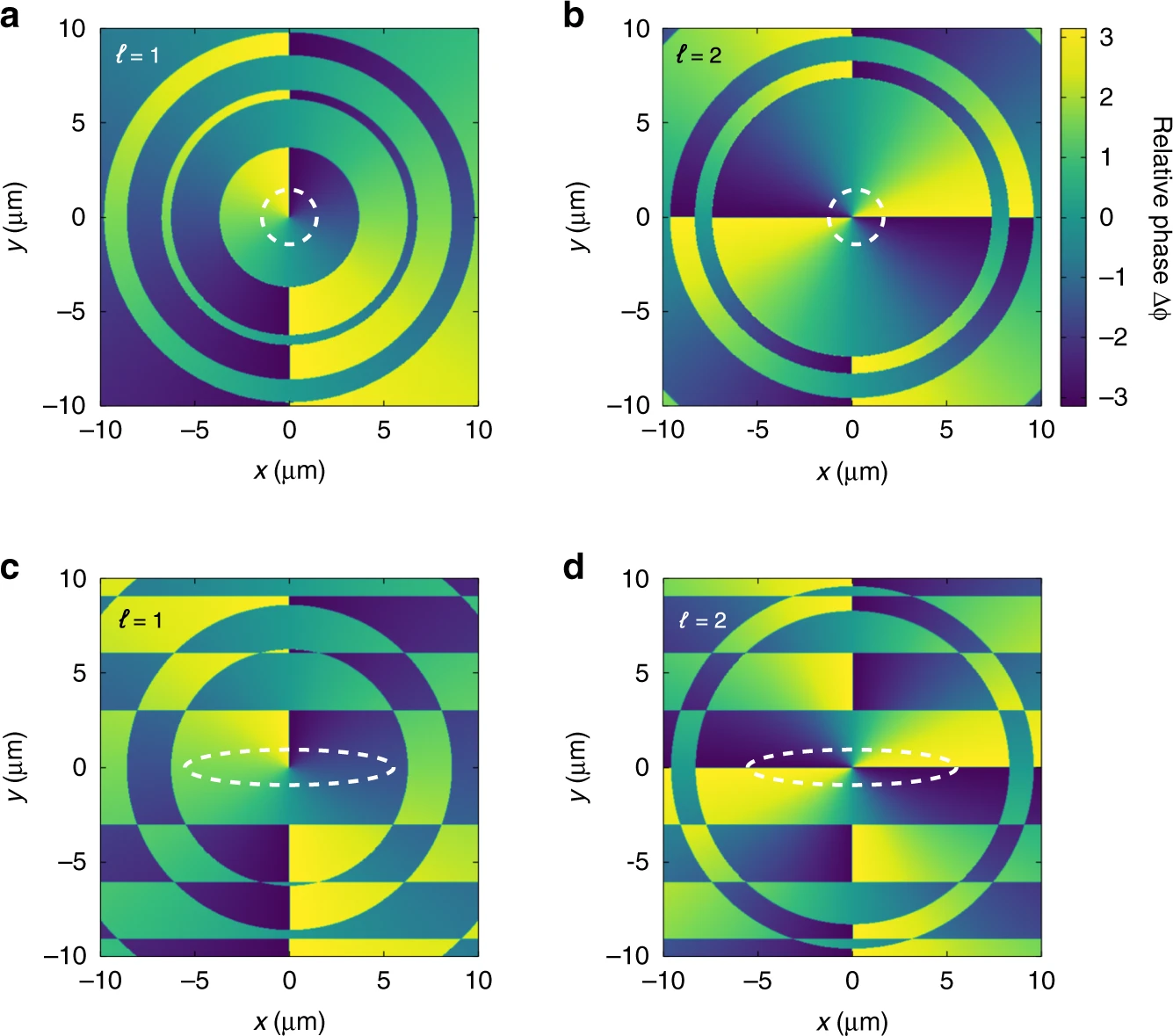
为了更详细地可视化涡旋脉冲的相位结构,关键是控制双色激光场的形态并重新分配焦点光斑中释放的光电子的权重。为此,研究人员在探测光路中使用了2 mm的水平狭缝,使探测场的圆柱形对称性和合成的双色激光场都可以被打破。
在这种情况下,当空间雕刻的探测光场(图1d2)与甜甜圈形状的未知脉冲(图1d4、d5)重叠时,合成场的强度分布水平拉伸。主导的光离区域也被拉伸(图3c, d中的虚线圈),因此,当使用这种双色激光场进行强场电离测量时,大部分光电子沿焦平面上的y=0线(标记为Δϕ|y=0)从局部相对相位释放出来。对ℓ= 1(图3 c),有Δϕ|y=0 = −π/2,和π/2。然而,对于ℓ=2(图3 d),它成为Δϕ|y=0 = −π和π。这种双色激光场相位分布的多样性源于光轨道角动量在ℓ=1和ℓ=2之间的奇偶数不同。注意:对于Δϕ|y=0 = −π/2和π/2,光电子动量分布中的新月形叶具有相反的偏转角。但由Δϕ|y=0 = −π驱动的月形叶,与π具有相同的偏转角度。
在实验上,研究人员利用空间雕刻的双色激光场测量了光电子动量分布。如图4a, b所示,ℓ= 1的光电子动量分布仍然是一个环空,而ℓ= 2的光电子动量分布将显示一个新月形的瓣。这两种完全不同的光电子动量分布为光脉冲轨道角动量的探测提供了可观测数据。这里,图4a中的环空的产生机理与图2b、c中的环空有部分不同。由于Δϕ|y=0 = −π/2和Δϕ|y=0 = π/2电离的光电子形成了两个偏转角度相反的月牙形叶,其中一个叶的最大产率恰好补偿了另一个叶的最小产率。因此,测量的总光电子动量分布仍然看起来像一个环空(图4a)。
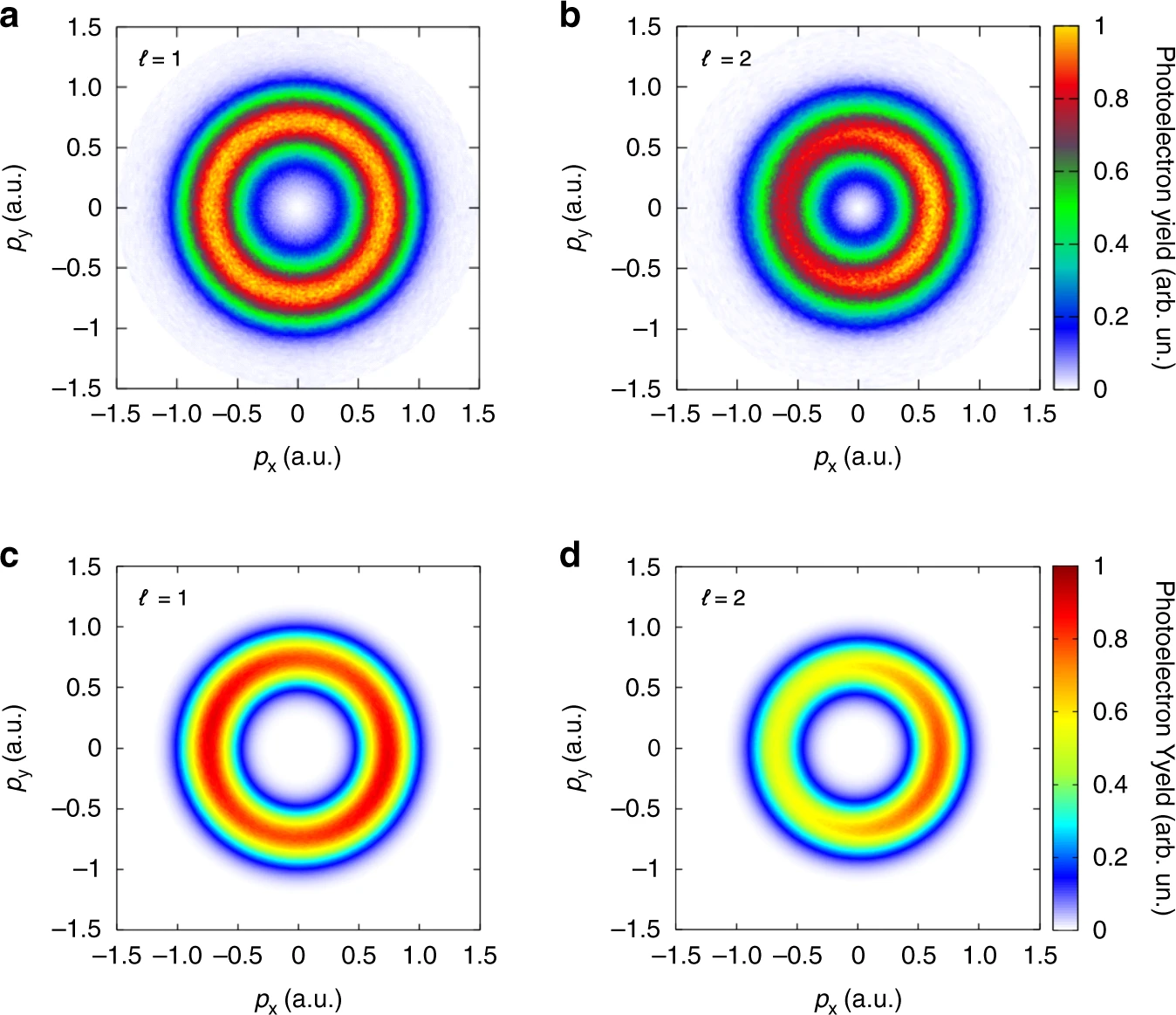
图4 用空间雕刻光场探测强涡旋脉冲的轨道角动量。(a,b)测量的光电子动量分布。(c,d)模拟光电子动量分布。400nm场的拓扑荷为(a,c)ℓ = 1和(b,d)ℓ = 2。
在实验中,由于涡旋场的轨道角动量信息是由这两个激光脉冲的重叠区域记录的,因此,大部分光电子都从重叠区域释放。这里,如果狭缝宽度太大,聚焦探测脉冲的水平尺寸将小得多。一旦探测脉冲的焦点水平尺寸短于未知脉冲的圆环形状的径向距离,则从两个光场的重叠区域释放的光电子的产率将降低,从而可能影响轨道角动量探测精度。
为进一步支持检测方案,研究人员使用经典轨迹蒙特卡罗模型进行了模拟,其中充分考虑了双色激光场的轨道角动量诱导的空间强度结构和螺旋相位结构。在模拟中,从焦平面不同点释放的光电子在动量空间中非相干叠加。如图4c,d所示,模拟结果与实验观察结果吻合良好。因此,未知脉冲的轨道角动量ℓ = 1和ℓ = 2可以通过控制探测光的轮廓来清楚地表征。此外,从理论上表明,探测光束的轨道角动量和自旋角动量的手性为测量光学涡旋的轨道角动能提供了强大的工具箱。
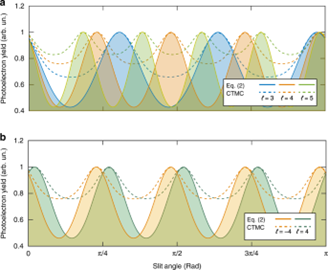
在不丧失一般性的情况下,研究人员使用400 nm平面波作为探测脉冲,800 nm涡旋脉冲作为携带各种轨道角动量的未知脉冲。通过计算Wʹ(φs),如图5a所示,当改变狭缝角度时,不同的轨道角动量值,Wʹ的最大值是不同的。值得注意的是,极大值的数量恰好等于拓扑荷的值。极值相位可以清晰地反映轨道角动量值的符号,如图5b(实线)所示。为了支持该方案,研究人员还使用经典弹道蒙特卡罗模型(图5a, b中虚线)进行了仿真。如图所示,经典弹道蒙特卡罗模型的结果与解析方法具有很好的一致性。特别地,这两种方法计算出的极值位置具有很好的一致性。在这里,可以发现这两个模型的结果的最大值和最小产率的对比存在偏差。在解析方法中,电子在隧道出口的初始动量被丢弃,而在经典轨迹蒙特卡罗模型中,初始横向动量被选择为以零为中心的高斯分布。因此,如图5所示,经典轨迹蒙特卡罗模型得到的最大和最小产率的对比小于解析模型得到的最大值和最小产率的对比。
02
在光离过程中,由于强光场中的光斑与电子质动力运动存在较大差异,电子无法“看到”驱动激光场的全局几何结构。因此,很难直接体现光离过程中电子动力学的光轨道角动量。为了克服这一困难,研究人员采用了合成的双色同向旋转圆激光场结构。在这个几何图形中,可以清楚地揭示光轨道角动量在强场电离中的作用。值得注意的是,光离信号对相互作用的激光场的偏振状态也很敏感。因此,该方法有潜力进一步表征更复杂的激光场,如矢量光场和更复杂的光学天文光束。
研究人员提出的光离方法与传统的光学方法有本质的区别。光电子动量分布和产额可以直接记录涡旋脉冲的空间相结构信息。在实验中,研究人员控制每个光脉冲只电离一个原子。氩原子的第一电离势为Ip = 15.8 eV,电离电子Ek的最大可模拟发射能约为7 eV(图2)。800 nm和400 nm光场的光子能量分别为ω800 = 1.55 eV和ω400 = 3.1 eV。假设吸收的800 nm光子和400 nm光子的数量分别为n800和n400。根据能量守恒,则有: n800ω800 + n400ω400 = Ip + Ek。虽然有不同的吸收光子通道(n800, n400),可以很好地推测,从激光脉冲吸收的光子数约为n800 + n400 约为10,这与每个激光脉冲的光子总数(>1015)相比是非常微不足道的。即,探测过程对激光轨道角动量状态几乎没有影响。这种独特的特性使光离方法成为测量光学系统量子态,如光子的轨道角动量或自旋角动量的理想而独特的工具。所测光学系统具有广阔的应用前景。
总之,研究人员展示了一种基于强场电离过程的高强度激光脉冲轨道角动量的新检测方案。在该方案中使用了合成的双色共旋转圆形激光场配置,其中使用平面波作为探测光来可视化其他涡旋脉冲的轨道角动量。为了支持这种情况,研究人员给出了实验和理论结果。目前,该方法可能是在强光-物质相互作用中原位检测光脉冲轨道角动量的唯一充分方法。这项研究中使用的方法可以扩展到使用强涡旋脉冲控制高阶谐波产生中的极端紫外辐射,这可以在很大程度上促进对高能光子辐射的时空控制。此外,这项研究还对产生和探测结构化电子束(如电子涡旋)有意义。
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。







