OCT:从原理到关键参数
一、
什么是OCT?
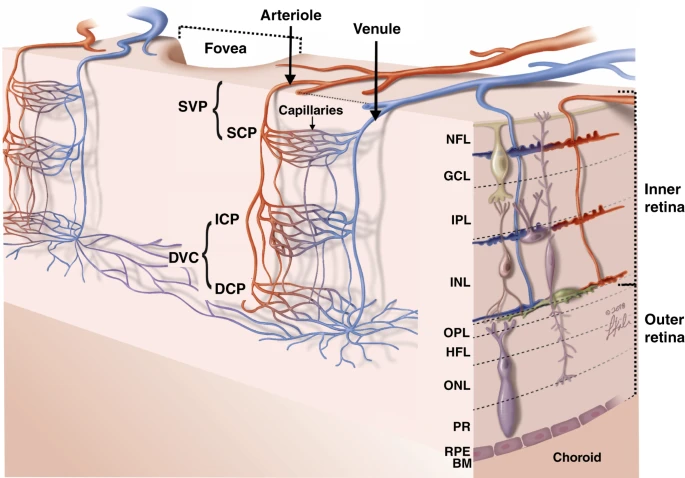
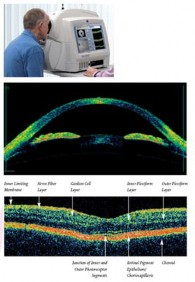
光学相干断层扫描(OCT)是一种三维成像技术,可以在散射介质中进行高分辨率成像,无需接触样品或使用任何耦合介质。OCT的横向成像分辨率可达到几微米,成像深度可达几毫米。OCT能够提供样品表面轮廓和次表面结构(即表面以下的结构)及样品均匀性的信息,从而实时提供准确的信息用于诊断、监测和现场过程反馈。因此,OCT已经在眼科、皮肤科、血管造影等生物成像领域得到了应用,并且在材料检测和无损检测中作为超声波的强大替代技术。
二、
OCT的工作原理
OCT依赖于样品不同区域的背向散射光来生成3D图像。它使用不同的定位技术来获取轴向(沿光束方向或进入样品的z轴)和横向(垂直于光束的平面或样品的x-y轴)信息。轴向信息是通过估计从样品中的结构或层反射的光的时间延迟来获得的。这种技术类似于生成超声波图像的技术,但使用的是光而不是声音。由于光速极快,直接测量反向散射光的时间延迟并不容易。因此,OCT系统使用低相干干涉技术间接测量时间延迟。
01
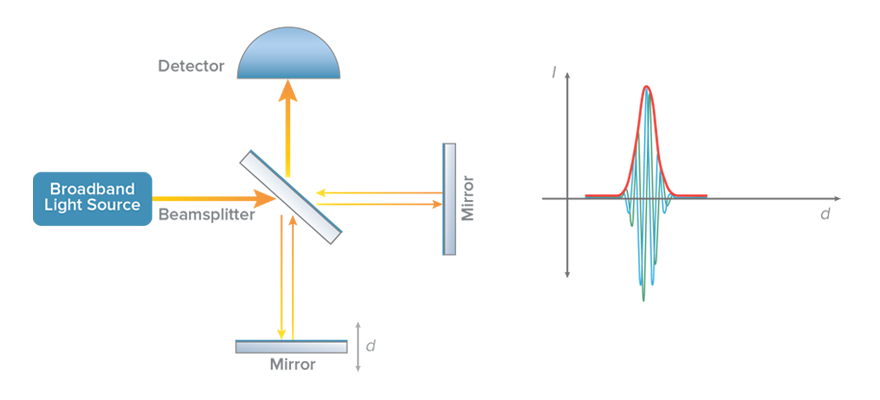
移动参考臂实现OCT测量
在低相干干涉仪中,使用具有宽光谱带宽的光源进行照明。光源发出的光被分束器分成两条路径,称为参考臂和样品臂。来自每条臂的光被反射并在检测器处结合。只有当参考臂和样品臂的光程几乎相等时,检测器上才会出现干涉效应。因此,干涉现象的出现可以被用来进行光程的相对测量。
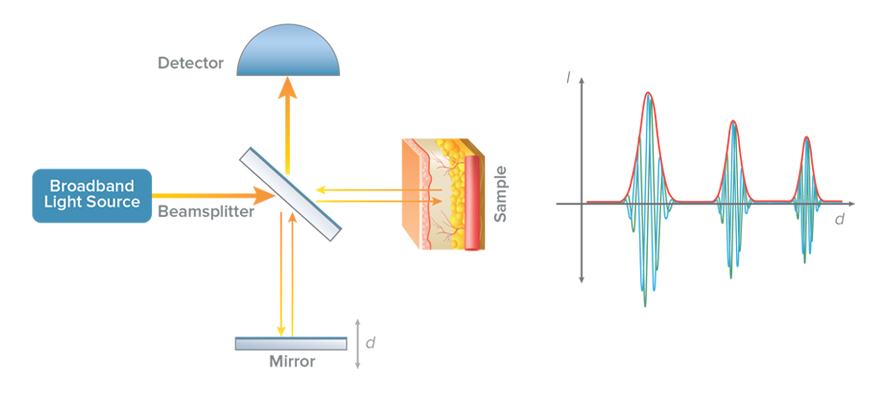
光学相干断层扫描就是将样品臂中的镜子替换为待成像的样品。然后对参考臂进行扫描,并在检测器上记录得到的光强度。当镜子几乎与样品中的某个反射结构等距时,会出现一定的干涉图案,从而获得样品对应位置的结构信息。显然在参考镜移动的过程中,两次干涉发生对应的参考镜位置之间的距离对应于测量光路中样品两个反射结构之间的光学距离。当光束穿过样品时,不同的位置的独特结构会通过上述低相干干涉记录的反射量被记录下来,从而得到测量样品的散射信号和深度之间的函数关系。
把 OCT 中使用的宽带光源光束聚焦到一个小点(约几微米),并在样品上进行x-y扫描,同时使用干涉测量收集深度信息,这样可以构建样品的完整 3D 图像。
02
傅里叶域OCT
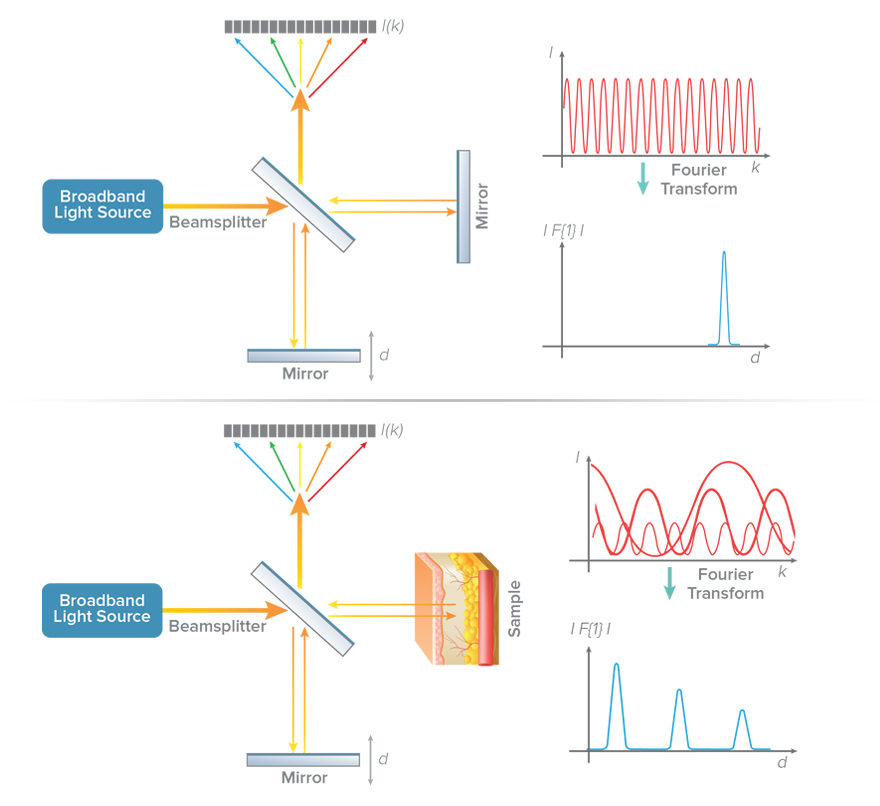
傅里叶域OCT(FD-OCT)提供了一种更高效的方法来实现上述低相干干涉。傅里叶域OCT(FD-OCT)并不是像上边提到方法那样在参考镜的不同位置记录强度,而是将强度记录为光的波长(或频率=光速/波长)的函数。不同频率的光强度变化率反映样品中不同反射层的位置信息。可以证明,光谱干涉数据的傅里叶变换提供的信息相当于移动参考镜所获得的信息。
03
傅里叶域OCT测量光谱干涉的两种常用方法
光谱域光学相干断层扫描(SD-OCT:Spectral Domain Optical Coherence Tomography):宽带光源向样品发出包含很多多波长成分的光谱管,并使用光谱仪同时测量所有波长。
·扫频源光学相干断层扫描(SS-OCT:Swept Source Optical Coherence Tomography):光源在一系列波长范围内进行扫频,检测器的时间输出被转换为光谱干涉。
傅里叶域OCT相对于干涉仪中样品臂镜的移动拥有更快的成像速度,因为样品的所有反射都被即时的同时测量出来的。傅里叶域OCT引入的速度提升为该技术开辟了全新的应用领域。通过商业化的设计,傅里叶域OCT可以轻松获得实时视频、面下OCT成像,使其广泛用于用于诸如过程监控和手术引导等对实时性要求比较高的领域之中。
三、
OCT系统的关键参数
01
分辨率
OCT系统的轴向和横向分辨率是独立的。
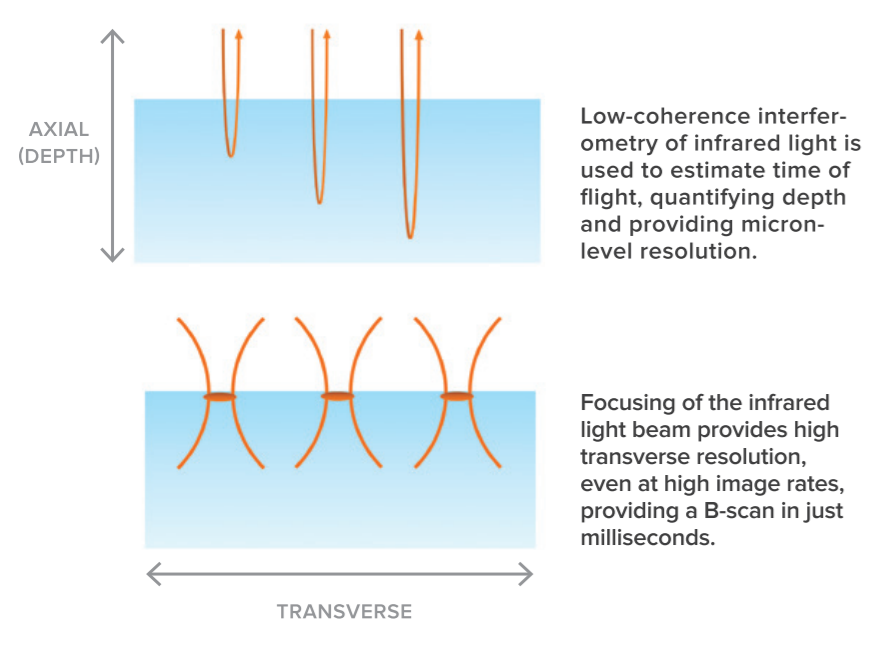
轴向(深度)分辨率与光源的带宽(相干长度)有关。对于高斯形光谱,轴向分辨率 (λc) 由以下公式给出:

其中:λ是中心波长,Δλ 是光源的带宽。
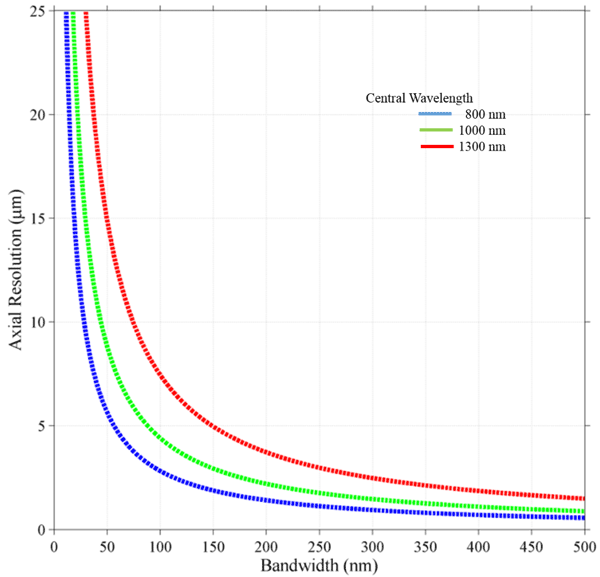
需要注意的是,这个光谱是指在探测器上测量到的光谱,可能与光源的发射光谱不同,这是由光学元件和探测器本身的响应造成的影响所致。需要注意的是,严格来讲上述公式仅适用于高斯形光谱,对于其他光谱形状仅可作为一个分辨率估算参考。对于任意已知形状的光谱,应估算轴向扩展函数以了解可实现的分辨率和可能的边带。下图中的轴向分辨率方程的图显示了三个不同中心波长的情况,展示了光源带宽对近红外常用工作带中的轴向分辨率的影响。
02
成像深度
OCT(光学相干断层成像)的成像深度主要受光源在样品中的穿透深度限制。此外,在傅里叶域OCT中,深度还受到光谱仪有限像素数和光学分辨率的限制。如前所述,傅里叶域OCT中的图像是在傅里叶变换光谱干涉数据后获得的。傅里叶变换后的总长度或深度受光谱数据采样率的限制,并遵循奈奎斯特定理。
具体来说,光谱数据采样率(或采样密度)指的是在给定的波长范围内,光谱仪所能分辨和记录的波长点的数量。更高的采样密度意味着在相同的波长范围内有更多的采样点,从而可以获得更高的分辨率和更大的成像深度。
由N个像素采样的总带宽(Δλ)给出了波长采样率δλ = Δλ/N。由于傅里叶变换将频率与时间关联起来,我们可以将波长转换为频率,δν = cΔλ /λ²。奈奎斯特定理表明,傅里叶变换数据中的最大时间延迟将是tmax = 1/2 δν,而数据中的最大深度将是zmax = c* tmax。通过结合这些,傅里叶域OCT中可实现的最大成像深度为:
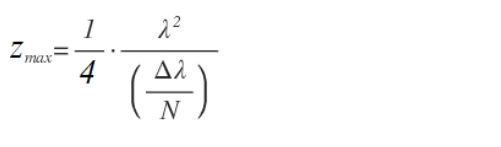
03
灵敏度随深度的变化关系
在傅里叶域OCT中,理论上灵敏度取决于反射目标的位置。最大灵敏度出现在样品光和参考光之间光程正好相等的点,即零延迟差点附近,并且随着我们远离零延迟点而减小。这种损失是由光谱仪的有限像素大小和有限光学分辨率导致的。可以证明,灵敏度与深度的关系如下:
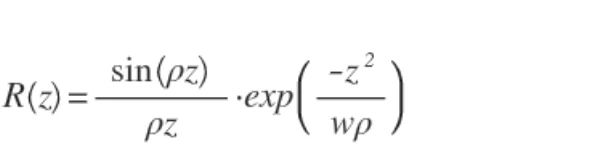
其中
R(Z):随深度变化的灵敏度。
z: 深度,通常指光在样品中传播的距离。
ρ: 一个与光谱仪分辨率和光源带宽相关的常数,具体定义依赖于系统的设计。
W=δλ/Δλ: 其中δλ是波长采样率(光谱仪的分辨率),Δλ是总带宽
sin(ρz): 表示由于光谱仪有限像素引起的调制效应。
sin(ρz)/(ρz): 表示由于有限像素引起的调制效应的归一化形
exp[-z^2/(wρ)] : 指数衰减项,表示由于光谱仪有限光学分辨率引起的衰减效应。
通过这个公式可以看出,OCT的灵敏度随着分子深度z^2的增加而减小,这种减小是由光谱仪的有限像素和光学分辨率共同决定的。
04
信噪比
信噪比一般定义为信号功率与噪声功率的比率,噪声功率用其方差来定义。OCT的主要噪声来源有:
A,探测器噪声,主要来自电子元件的热波动。
B,由于光子到达和探测器检测的内在方差产生的散粒噪声。
C,光源的相对强度噪声 (RIN)。
理想的OCT系统,应该是其探测器和强度噪声都被最小化掉了,在散粒噪声域内工作,其性能仅受限于到达探测器的光子数量。
05
OCT的灵敏度
在光学相干断层扫描 (OCT) 中,灵敏度指系统检测样本反射最微弱信号的能力。数值上,灵敏度是使信号达到信噪比 (SNR) 为1时的信号衰减程度,即信号强度等于系统固有噪声的点。
06
分贝 (dB) 单位的测量
信噪比或灵敏度常用分贝 (dB) 表示。物理量的dB单位对应10log(Pa/Pb)。光学测量中,光功率 (P) 与光电探测器输出电流 (I) 成正比,但电功率与I²成正比,因此考虑光功率时,OCT的SNR和灵敏度测量用20log(Pa/Pb)。
07
速度
OCT系统的速度取决于到达探测器的光量。速度与系统积累足够光子的时间直接相关。其他限制因素包括各部件自身参数的限制,例如:基于光谱仪的光谱域OCT系统速度受相机传感器和电子元件限制。对于扫频光源傅里叶域OCT,扫频激光源的速度常是限制因素。尽管SS-OCT常因速度被选择,近年来相机速度的进步开始缩小这一差距。