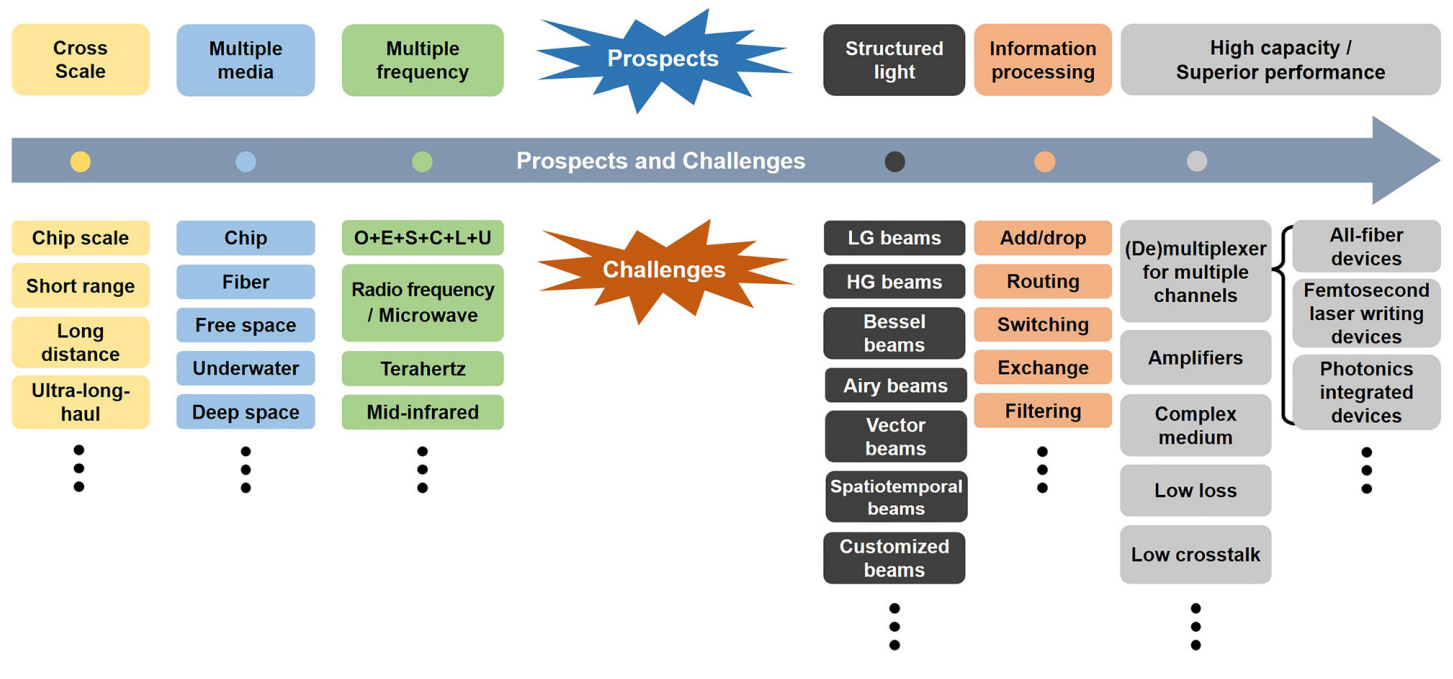
轨道角动量可用于实现高容量数据传输系统,可应用于经典和量子通信。在此,Nelson Villalba等人通过实验研究了环芯光纤中完美涡旋光束和拉盖尔-高斯光束的产生和传输,并评估了它们在通信和量子应用中的传输特性。研究表明,当使用单一制备阶段时,完美的涡旋光束呈现较小的环半径变化,从而允许将更高的光功率耦合到环芯光纤中。这些结果导致使用轨道角动量建立基于光纤的通信链路所需的功率降低,并为未来在空分多路复用光纤上实现高维量子通信奠定了基础。该工作发表在Optics Express上。
Nelson Villalba, Cristóbal Melo, Sebastián Ayala, Christopher Mancilla, Wladimir Valenzuela, Miguel Figueroa, Erik Baradit, Riu Lin, Ming Tang, Stephen P. Walborn, Gustavo Lima, Gabriel Saavedra, and Gustavo Cañas, Transmission of optical communication signals through ring core fiber using perfect vortex beams, Optics. Express 31(24): 40113-40123 (2023).
为了增加光纤通信系统的容量,多年来人们一直利用光的波长(频率)、偏振、幅度和相位等物理特性来复用信息。然而,由于硅基光纤的非线性特性,数据容量正在达到其目前的极限。到目前为止,使用上述所有物理维度已经实现了超过54公里的244.3 Tb/s的传输。为了进一步提高光纤的信息承载能力,需要利用新的自由度,其中使用扩展的光纤带宽和额外的空间模式是一些最有前途的解决方案。空分复用已被引入作为一种可行的空间域多路复用的方法,并发展了新的光纤类型来支持多种空间模式的传输。目前,支持空分复用的光纤的例子包括多芯光纤、少模光纤和多模光纤以及环芯光纤。
光学轨道角动量可以与用eilθ描述的螺旋相位前的光束相关,其中,θ是圆柱坐标系中的方位角,l可以取整数值,通常称为拓扑荷。由于沿其传播轴的相消干涉产生了一个暗区,因此,轨道角动量模式的强度分布特征为甜甜圈形状。近年来,光的轨道角动量复用是研究的热点,在自由空间和基于光纤的光通信系统中引起了极大的兴趣。具有不同拓扑荷的轨道角动量征模在相关的希尔伯特空间中形成一个正交基。此外,原则上轨道角动量模式的数量可以是无限的,因此,它们有可能增加每个光子携带的信息容量。
迄今为止,轨道角动量已被用于建立经典通信链路,在1.1 km光纤链路上使用轨道角动量复用实现了1.6 Tb/s的传输,在自由空间数据链路上通过轨道角动量、偏振和波长的三维复用实现了100 Tb/s的传输。实现基于轨道角动量的空分复用系统的主要困难是轨道角动量模式在光纤中的传播和耦合。首先,为了在光纤中传播轨道角动量模式,光纤应在矢量模式之间呈现较大的有效折射率分离,并具有与轨道角动量场兼容的折射率分布。这两种情况都可以使用环芯光纤来实现。其次,将大量轨道角动量模式耦合到环芯光纤中仍然是一项具有挑战性的任务。对于自由空间传输,拉盖尔-高斯模式是一种自然的选择,因为它们在自由空间传播过程中保持其横向结构。然而,这些模式的甜甜圈形强度分布取决于光束的拓扑荷。因此,大多数轨道角动量光束在环芯光纤中传播的实验实现使用两种模式,要么具有相同的拓扑荷,值为±l,要么具有不同的拓扑荷,但光束直径相似。这一限制决定了基于轨道角动量的大型空分复用系统的实际实现,从而增加了该技术可实现的容量。为了解决这一问题,研究人员从理论上提出了利用完美涡旋光束来有效地在环芯光纤中耦合轨道角动量模式。完美涡旋光束是一种轨道角动量模式,无论拓扑荷如何,它都具有几乎恒定的强度半径,可以通过贝塞尔-高斯模的傅里叶变换进行数学计算得到。
将轨道角动量耦合到光纤中
为了在光纤中传播轨道角动量光束,需要激发具有相同传播常数的光纤本征模态,以保证没有模态偏离影响轨道角动量模态。具有单个高折射率环的环芯光纤可以支持径向基模,使其成为轨道角动量光束传输的合适平台。虽然使用环芯光纤可以在传输过程中保持轨道角动量模式,减少模式串扰,但高折射率环的尺寸和掺杂特性将决定环芯光纤支持的最大模式数。光纤支持的轨道角动量模式可以描述为光纤支持的线偏振模式或矢量模式的线性组合。
拉盖尔-高斯模式是一组通常用于通信的轨道角动量模式,其特征是指数p和l,它们分别是径向指数和轨道角动量值。为了使用拉盖尔-高斯模式将轨道角动量模式耦合到光纤中,使用径向指数p=0的拉盖尔-高斯模式,其对应由单个环组成的强度分布。然而,由于拉盖尔-高斯模的环半径以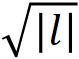 为尺度,使用这些拉盖尔-高斯模会导致不同轨道角动量值下的耦合效率不同。另一方面,完美涡旋光束模态具有一个环状的强度分布,其半径随轨道角动量值的函数变化要小得多。因此,对于给定的一组轨道角动量值,与拉盖尔-高斯模式相比,使用完美涡旋光束来耦合进入光纤的轨道角动量光束应该具有更高的总体效率。
为尺度,使用这些拉盖尔-高斯模会导致不同轨道角动量值下的耦合效率不同。另一方面,完美涡旋光束模态具有一个环状的强度分布,其半径随轨道角动量值的函数变化要小得多。因此,对于给定的一组轨道角动量值,与拉盖尔-高斯模式相比,使用完美涡旋光束来耦合进入光纤的轨道角动量光束应该具有更高的总体效率。
为了生成完美涡旋光束,需要一种能够实时控制每个光束参数的方法,可通过印在空间光调制器和光透镜上的计算全息图在自由空间中产生完美涡旋光束。此外,研究人员提出了一种替代方法,该方法使用全息图的菲涅耳域图形的计算全息图来实现傅里叶变换,而无需在此过程中使用透镜。然而,这种方法有一个缺点,即高阶噪声场的贡献在编码信号的傅里叶变换平面中出现削弱。使用复标量场、所需完美涡旋光束和光学透镜的正确编码,可以创建用于加载在纯相位空间光调制器上的计算全息图,数学描述为:
 (1)
(1)
其中,r和θ是圆柱系统中的径向和方位坐标,l是轨道角动量光束的拓扑荷,ω0是完美涡旋光束的束腰,ωg是入射到空间光调制器上的高斯场的束腰,rr是完美涡旋光束的环半径,Il(·)是第一类一阶修正贝塞尔函数。此外,rr可以通过rr = krf/k使用径向波数(kr)来定义,其中,f是允许进行傅里叶变换的透镜的焦点,k是光束的波数。在实验中,参数kr可以作为一个可调参数来保持完美涡旋光束模式下的恒定环半径。
类似的技术可以用来产生拉盖尔-高斯光束。在这种情况下,复标量场的横向空间轮廓由以下方程给出:
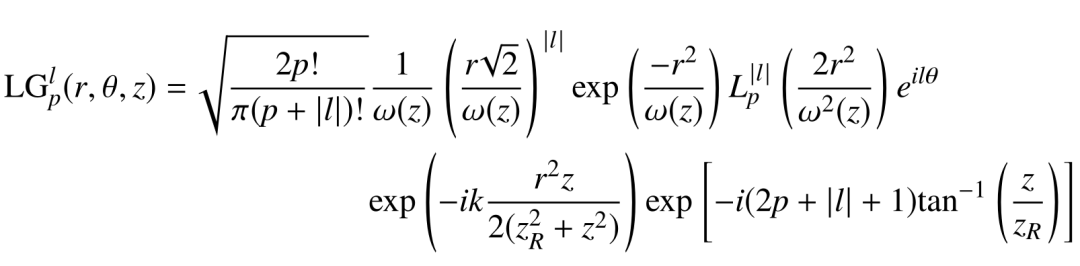 (2)
(2)
其中,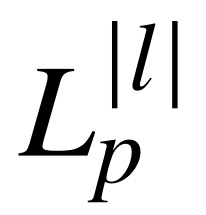 为关联的拉盖尔多项式,l和p分别为方位角指数和径向指数,zr为瑞利范围,ω(z)为束腰(在这里,被认为是常数)。p参数与拉盖尔-高斯模式下横向剖面中同心环的数量有关。这里,研究了当径向参数固定在p=0时,仅用一个环半径的轨道角动量模式耦合到环芯光纤中的情况。(2)式采用与完美涡旋光束相同的坐标进行描述,并在光束传播方向上添加z坐标。
为关联的拉盖尔多项式,l和p分别为方位角指数和径向指数,zr为瑞利范围,ω(z)为束腰(在这里,被认为是常数)。p参数与拉盖尔-高斯模式下横向剖面中同心环的数量有关。这里,研究了当径向参数固定在p=0时,仅用一个环半径的轨道角动量模式耦合到环芯光纤中的情况。(2)式采用与完美涡旋光束相同的坐标进行描述,并在光束传播方向上添加z坐标。
研究中用于产生、传输和测量完美涡旋光束的实验装置,如图1所示。每个阶段都用一种颜色突出显示,蓝色用于准备,橙色用于传输,绿色用于测量。使用商用SFP+收发器产生和检测光信号。SFP+收发器是强度调制直接检测设备,其中信息被调制成光场的强度。它使用开关键作为调制格式,符号速率为1 GBd。该收发器由现场可编程门阵列驱动,其长度为237的伪随机二进制序列。发射机采用以1550 nm为中心的光源,通过掺铒光纤放大器和可变光衰减器对信号功率进行放大。随后,将光信号发射到自由空间,准直后通过半波片和偏振分束器,在空间光调制器前制备入射光束,为简单起见,如图1所示。
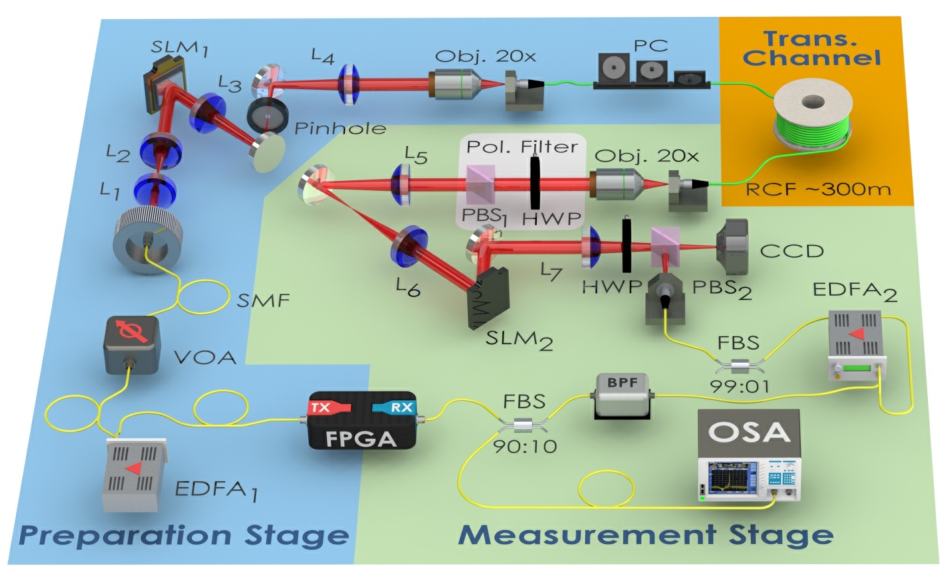
图1 实验装置。蓝色、橙色和绿色背景分别代表准备阶段、传输阶段和测量阶段。 传统色散傅立叶变换的原理,并结合色散傅立叶变换和光谱干涉。
当水平偏振高斯光束(ωg≈1140 µm)被纯相位空间光调制器(SLM1)反射时,产生轨道角动量光束模式。纯相位空间光调制器使用期望的轨道角动量光束模式加载计算全息图。纯相位空间光调制器反射的光束穿过由两个透镜(L3和L4,f3=f4=150 mm)组成的4f共焦光学系统,透镜与透镜之间有一个针孔。针孔滤除计算全息图的第一阶衍射,从而将生成的轨道角动量光束模式放置在该光学系统的像面上。轨道角动量光束模式耦合到环芯光纤中,用于传播信号。为了耦合轨道角动量光束模式,使用20倍物镜。环芯光纤的内半径和外半径分别为a=6 µm和b =9 µm,其总长度为300 m。采用基于环芯光纤的偏振控制器控制光纤的轨道角动量光束模式。在轨道角动量光束模式通过环芯光纤传播后,使用第二个20倍物镜来产生离开纤芯的轨道角动量光束的图像。该光学系统将模半径放大33倍,以达到rr≈230 µm。在光纤输出处使用一个由半波片和偏振分束器组成的偏振滤波器,以确保轨道角动量光束的水平偏振。
利用第二个4f共聚焦光学系统(L5和L6)对轨道角动量光束放大2倍,允许在SLM2上产生轨道角动量光束的图像。在SLM2上,研究人员部署了一组分叉全息图(拉盖尔-高斯模式为基础的计算全息图),一次一个,编码一个相对于SLM1的共轭轨道角动量值。最后,利用偏振分束器选择将信号发送到CCD相机还是耦合到单模光纤进行检测。单模光纤被放置在最后一个透镜(L7)的傅里叶变换平面的中心。为了检测传输序列,通过掺铒光纤放大器对信号进行放大和滤波,去除带外放大的发射噪声。使用光谱分析仪记录接收到的频谱和功率。在光接收机上,现场可编程门阵列用于确定误码率。
为了研究轨道角动量模式的产生,研究人员利用空间光调制器和4f光学系统分别产生了完美涡旋光束和常规拉盖尔-高斯光束。在光纤耦合系统之前,使用CCD相机将产生的光束强度记录在前4f光学系统(L3和L4)的成像平面上(图1)。在空间光调制器上使用计算全息图产生的轨道角动量光束,如图2(a)所示,其中显示了每个模式阶数l的检测强度。当l的阶数从l=1增加到l=6时,完美涡旋光束的环半径保持不变,而拉盖尔-高斯束的环半径变化较大。完美涡旋光束和拉盖尔-高斯模态的测量环半径,如图2(b)所示,其中拉盖尔-高斯模态的环半径在77-193 µm之间变化。当kr=3.06416时,平均环半径为147.9 µm。在这种情况下,观察到环半径的变化为29 µm,当l=6时,观察到的最大半径为165.9 µm。接下来,研究了kr参数对生成的完美涡旋光束环半径的影响,如图2(c)所示。
基于l=3时得到的kr=3.06416进行优化。然后,利用式(1)增大或减小kr以保持固定的环半径。在这种情况下,获得的平均环半径为140.5 µm,最大变化为4.7 µm。注意,与拉盖尔-高斯模式下观察到的环半径变化相比,在kr优化和没有kr优化的情况下的差异要小得多。例如,拉盖尔-高斯模式的环半径方差约为1873.3 µm2,而完美涡旋光束模式的环半径方差在kr优化和未kr优化时分别为5.4 µm2和122.1 µm2。因此,在不调整kr的情况下,拉盖尔-高斯模式的方差比完美涡旋光束模式高15倍。对于拉盖尔-高斯模式,众所周知,它们的半径随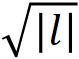 而增长,为了保持它们的环半径恒定,每个轨道角动量光束应该使用不同的光学系统。
而增长,为了保持它们的环半径恒定,每个轨道角动量光束应该使用不同的光学系统。
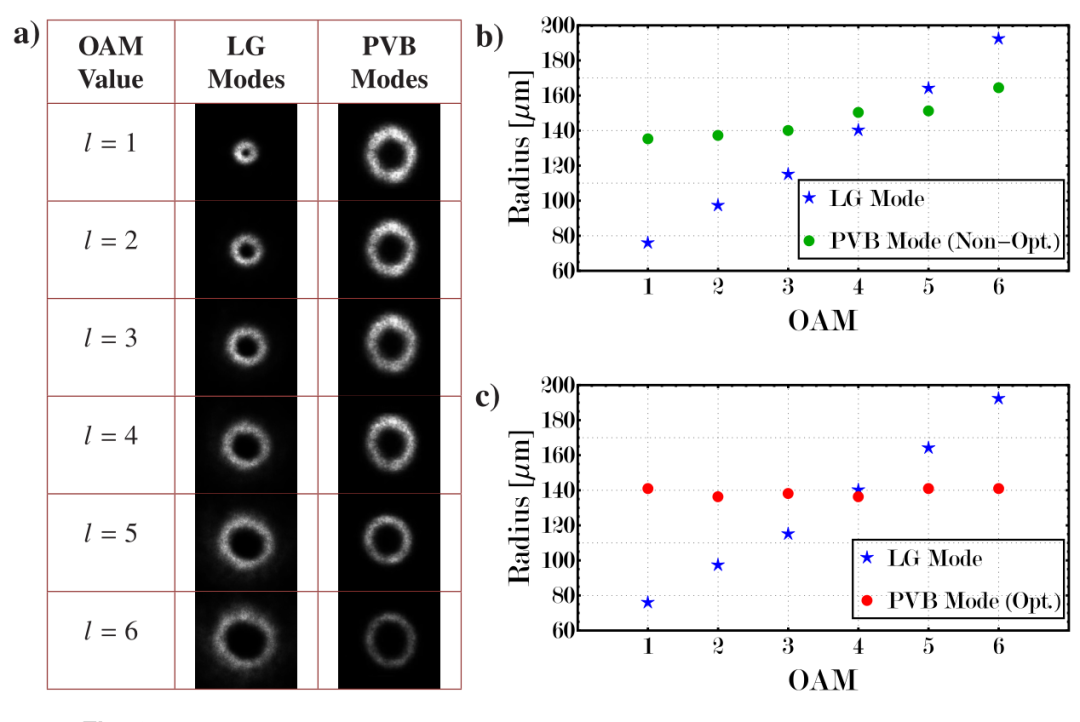
图2 a) 拉盖尔-高斯光束(第二列)和完美涡旋光束(第三列)生成的轨道角动量模态的横向强度分布图。b)和c) 表示完美涡旋光束模态环半径值与拉盖尔-高斯模态环半径值(两种情况下均为蓝星点)作为轨道角动量光束的拓扑荷值的函数的两个图形比较。b) 拉盖尔-高斯模式与完美涡旋光束未优化模式(kr固定,绿点)的比较,c) 拉盖尔-高斯模式与完美涡旋光束优化模式(kr可变,红点)的比较。
光纤中的轨道角动量模式可以用线偏振模式的线性组合来描述。研究人员使用的GRIN环芯光纤环芯光纤的内环半径为6 µm,外环半径为9 µm。环芯光纤支持最大l=4的轨道角动量模式传播。考虑到环芯光纤的环半径是固定的,为了保持所有模态的kr参数恒定,对生成的完美涡旋光束模式使用rr≈140 µm。在光纤输入端使用偏振控制器来控制光纤中线偏振模式的线性组合。在光纤输出处,评估了以下参数:场强度、轨道角动量模式与高斯模式之间的干涉以及光功率,如图3和4所示。图3显示了由光纤输入端的轨道角动量模式激发的LPa,b模式在光纤输出端的强度分布图。这是通过偏振控制器从弯曲扰动激发LPa、LPb或轨道角动量模式到通过环芯光纤传输的场来实现的。所传播的光纤模态独立于用来激发它们的自由空间光束,其差异来自于耦合模态的强度。此外,还显示了从环芯光纤发射的轨道角动量模式以及显示轨道角动量模式成功传播的高斯波束干涉图。
利用光纤输出端的接收功率表征了计算全息图与环芯光纤产生的轨道角动量模式之间的耦合效率。在两个轨道角动量模式(拉盖尔-高斯模式和完美涡旋光束, Pin≈450 µW)下,在第二个物镜的像面上测量光功率(20倍,图1),使用恒定耦合功率进入环芯光纤。完美涡旋光束模式的平均输出功率为 ≈16 µW,拉盖尔-高斯模式的平均输出功率为
≈16 µW,拉盖尔-高斯模式的平均输出功率为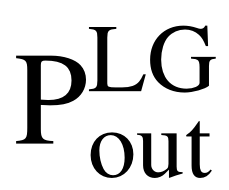 ≈3.32 µW。结果表明,完美涡旋光束模式的耦合效率高于拉盖尔高斯模式。为了验证通过环芯光纤传播的轨道角动量模式,研究人员对轨道角动量光束和高斯光束之间进行干涉实验。图3所示的干涉图定性地验证了轨道角动量光束通过环芯光纤有效地传播,其l值为l=1,2,3,4。
≈3.32 µW。结果表明,完美涡旋光束模式的耦合效率高于拉盖尔高斯模式。为了验证通过环芯光纤传播的轨道角动量模式,研究人员对轨道角动量光束和高斯光束之间进行干涉实验。图3所示的干涉图定性地验证了轨道角动量光束通过环芯光纤有效地传播,其l值为l=1,2,3,4。
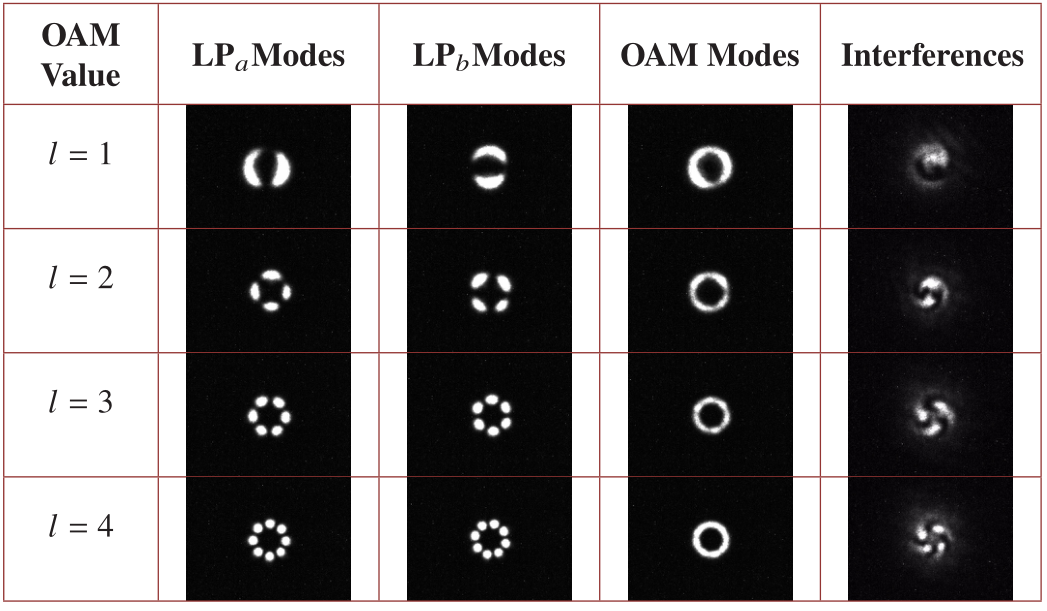
图3 通过环芯光纤传播的模式。第一列为LPa模式,第二列为LPb模式,第三列为轨道角动量模式,第四列为l=1至l=4的干涉模式。
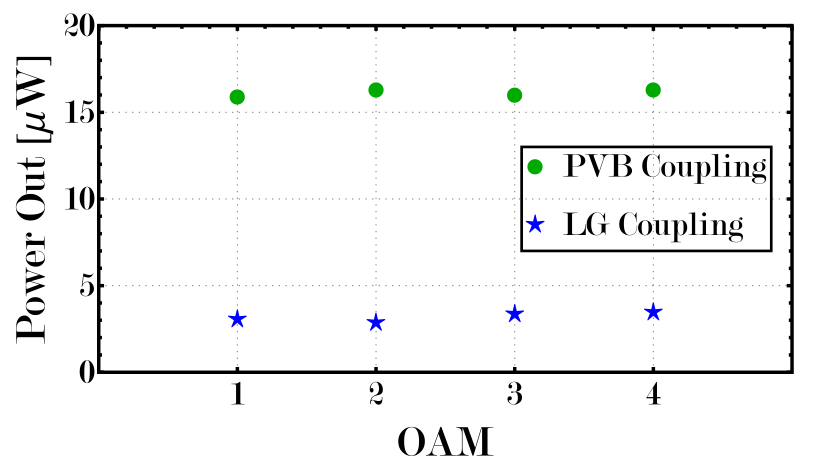
图4 采用不同耦合模式,完美涡旋光束模式(绿点)和拉盖尔-高斯模式(蓝星点),在第二物镜20倍像面上的环芯光纤输出功率测量值作为轨道角动量值的函数。
如前所述,轨道角动量被提出作为实现空分复用的一种方式来增加光纤通信系统的容量。考虑到这一点,使用完美涡旋光束将轨道角动量模式耦合到光纤中可以对系统产生积极影响,与拉盖尔-高斯模式相比,允许传输更长的距离,并简化了轨道角动量模式耦合系统的设计。在这里,研究人员使用工作在1 Gbps的商用SFP+转发器评估传输信号的质量。测量了光纤传输后的误码率。图5显示了在完美涡旋光束和拉盖尔-高斯模式下,当l=1,2,3,4时,测量到的误码率是耦合到环芯光纤中的功率的函数。与拉盖尔-高斯模式相比,完美涡旋光束需要更低的耦合功率来实现4.7×10-3的固定误码率。完美涡旋光束和拉盖尔-高斯模式的平均误码率的功率差为8.6 dB。此外,在固定的误码率下,完美涡旋光束在不同的l值下具有较小的性能差异,与拉盖尔-高斯模式的1.2 dB相比,观察到的差异为0.6 dB。从图5中可以看出,当l=2时,完美涡旋光束的性能最好,因为它需要最低的光功率来传输1 Gbps的信号。这一特性表明,完美涡旋光束是光纤空分复用系统中耦合调幅信息的更好候选者,可以实现具有类似功率要求的系统。

图5 在环芯光纤中使用完美涡旋光束(点)和拉盖尔-高斯模式(星点)测量传输后的误码率。连续的线条表示使用完美涡旋光束(青色)和拉盖尔-高斯模式(橙色)的误码率的对数平均值。紫色虚线表示HD-FEC阈值。
众所周知,在量子体系中,当使用更高维度的量子态时,一些量子信息协议可以更具鲁棒性,这些量子系统具有d>2个能级。携带轨道角动量的光子可用于编码轨道角动量量子,从而允许在通信双方之间传输更多信息。轨道角动量量子在量子信息协议中有无数的应用,包括在自由空间和光纤通道中,最著名的是量子密钥分发协议。特别是,环芯光纤在这种情况下已实现了其支持的轨道角动量模式可以用于增强经典和量子通信链路。
轨道角动量光束与环芯光纤的不对称耦合导致环芯光纤进行不期望的状态转换,从而导致高量子误码率(QBER)。量子误码率与用于量子密钥分发协议的量子态的平均保真度有关,如下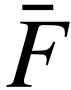 =1−QBER。在这里,研究人员用环芯光纤实验证明了四维轨道角动量编码量子系统可以高保真地通过300米的环芯光纤传播。为了保证量子密钥分发协议的无条件安全性,必须低于相干攻击(Dcoh)的量子误码率上限,这取决于所使用的量子系统的维度。在这种情况下,对于四维轨道角动量编码的量子系统,相干攻击的上限为Dcoh=18.96%。因此,平均保真度必须大于
=1−QBER。在这里,研究人员用环芯光纤实验证明了四维轨道角动量编码量子系统可以高保真地通过300米的环芯光纤传播。为了保证量子密钥分发协议的无条件安全性,必须低于相干攻击(Dcoh)的量子误码率上限,这取决于所使用的量子系统的维度。在这种情况下,对于四维轨道角动量编码的量子系统,相干攻击的上限为Dcoh=18.96%。因此,平均保真度必须大于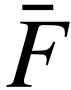 =0.81。图6显示了4维轨道角动量编码量子态通过环芯光纤传播后的测量保真度,平均保真度为92%。这为在空分复用光纤中使用高维轨道角动量编码量子态实现量子密钥分发协议铺平了道路。
=0.81。图6显示了4维轨道角动量编码量子态通过环芯光纤传播后的测量保真度,平均保真度为92%。这为在空分复用光纤中使用高维轨道角动量编码量子态实现量子密钥分发协议铺平了道路。
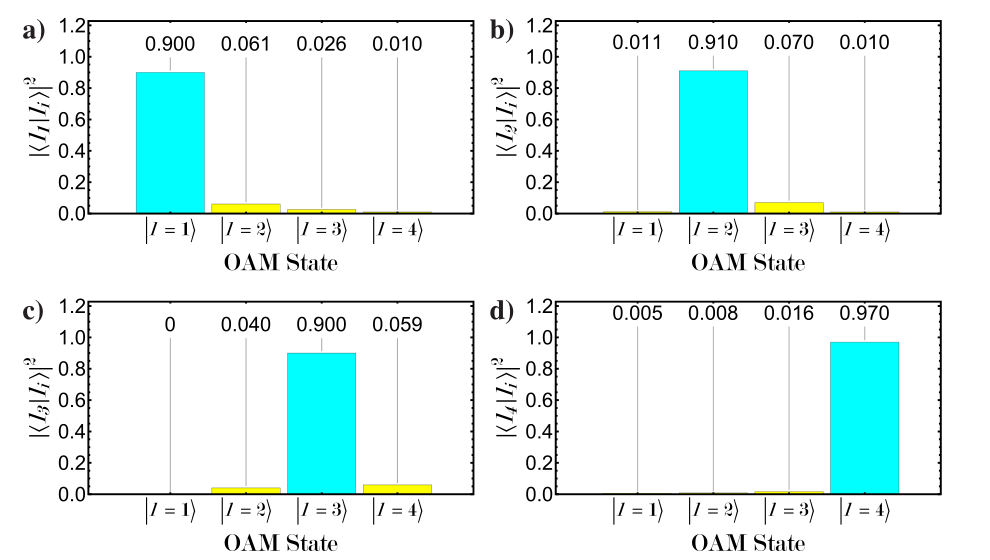
图6 在300米的环芯光纤中传播后的四个测量的保真度,对于状态a) |l=1⟩,b) |l=2⟩,c) |l=3⟩和d) |l=4⟩。该状态的平均保真度为92%。
总之,研究人员通过实验研究了环芯光纤中两束轨道角动量承载光束的产生和传输特性。所研究的光束是完美涡旋光束和拉盖尔-高斯光束。研究表明,当对所有轨道角动量光束使用单个准备阶段时,完美涡旋光束呈现较小的环半径变化且能够将更高的功率耦合到环芯光纤中。拉盖尔-高斯光束的环半径变化范围从77 µm到193 µm,而完美涡旋光束的环半径平均为140.5 µm,最大变化幅度为4.7 µm。此外,使用完美涡旋光束将更高的光功率耦合到环芯光纤中。完美涡旋光束和拉盖尔-高斯光束的平均耦合光功率分别为15 µW和4 µW。除了使用完美涡旋光束成功地将光学轨道角动量耦合到环芯光纤之外,研究人员还展示了建立以1 Gbps速度运行的传输链路的可能性。结果表明,完美涡旋光束的高耦合功率可以降低建立光纤通信链路所需的功率。与拉盖尔-高斯光束相比,使用完美涡旋光束所需的输入功率平均相差8.6 dB。此外,研究人员证明完美涡旋光束的恒定耦合功率作为模式阶数l的函数可以允许量子密钥分发协议的实现。这里的优点是测量的量子态保真度。此外,研究人员报告了在环芯光纤中传输后四维量子系统中的平均保真度为92%,这大于在相干攻击下成功分发密钥所需的最低保真度。因此,这项工作可以被视为发展完美涡旋光束作为通信光纤领先空分复用系统中的信息载体,并实现高维量子密钥分发系统的第一步。在这两种情况下,将轨道角动量光束更有效地耦合到环芯光纤中是增加信息容量的有力工具。

 (1)
(1)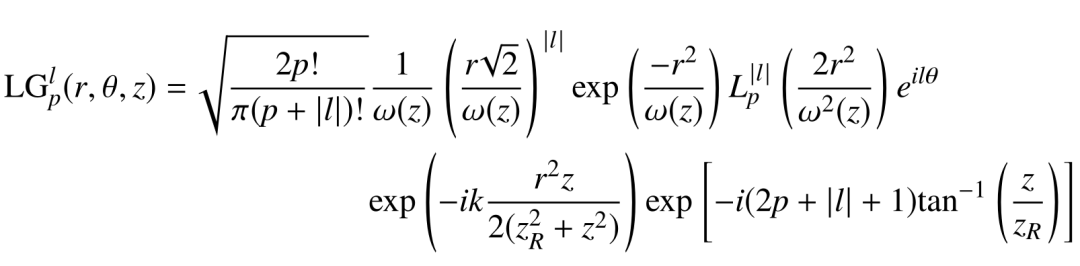 (2)
(2)![]() 为关联的拉盖尔多项式,l和p分别为方位角指数和径向指数,zr为瑞利范围,ω(z)为束腰(在这里,被认为是常数)。p参数与拉盖尔-高斯模式下横向剖面中同心环的数量有关。这里,研究了当径向参数固定在p=0时,仅用一个环半径的轨道角动量模式耦合到环芯光纤中的情况。(2)式采用与完美涡旋光束相同的坐标进行描述,并在光束传播方向上添加z坐标。
为关联的拉盖尔多项式,l和p分别为方位角指数和径向指数,zr为瑞利范围,ω(z)为束腰(在这里,被认为是常数)。p参数与拉盖尔-高斯模式下横向剖面中同心环的数量有关。这里,研究了当径向参数固定在p=0时,仅用一个环半径的轨道角动量模式耦合到环芯光纤中的情况。(2)式采用与完美涡旋光束相同的坐标进行描述,并在光束传播方向上添加z坐标。

![]() ≈16 µW,拉盖尔-高斯模式的平均输出功率为
≈16 µW,拉盖尔-高斯模式的平均输出功率为![]() ≈3.32 µW。结果表明,完美涡旋光束模式的耦合效率高于拉盖尔高斯模式。为了验证通过环芯光纤传播的轨道角动量模式,研究人员对轨道角动量光束和高斯光束之间进行干涉实验。图3所示的干涉图定性地验证了轨道角动量光束通过环芯光纤有效地传播,其l值为l=1,2,3,4。
≈3.32 µW。结果表明,完美涡旋光束模式的耦合效率高于拉盖尔高斯模式。为了验证通过环芯光纤传播的轨道角动量模式,研究人员对轨道角动量光束和高斯光束之间进行干涉实验。图3所示的干涉图定性地验证了轨道角动量光束通过环芯光纤有效地传播,其l值为l=1,2,3,4。


![]() =1−QBER。在这里,研究人员用环芯光纤实验证明了四维轨道角动量编码量子系统可以高保真地通过300米的环芯光纤传播。为了保证量子密钥分发协议的无条件安全性,必须低于相干攻击(Dcoh)的量子误码率上限,这取决于所使用的量子系统的维度。在这种情况下,对于四维轨道角动量编码的量子系统,相干攻击的上限为Dcoh=18.96%。因此,平均保真度必须大于
=1−QBER。在这里,研究人员用环芯光纤实验证明了四维轨道角动量编码量子系统可以高保真地通过300米的环芯光纤传播。为了保证量子密钥分发协议的无条件安全性,必须低于相干攻击(Dcoh)的量子误码率上限,这取决于所使用的量子系统的维度。在这种情况下,对于四维轨道角动量编码的量子系统,相干攻击的上限为Dcoh=18.96%。因此,平均保真度必须大于![]() =0.81。图6显示了4维轨道角动量编码量子态通过环芯光纤传播后的测量保真度,平均保真度为92%。这为在空分复用光纤中使用高维轨道角动量编码量子态实现量子密钥分发协议铺平了道路。
=0.81。图6显示了4维轨道角动量编码量子态通过环芯光纤传播后的测量保真度,平均保真度为92%。这为在空分复用光纤中使用高维轨道角动量编码量子态实现量子密钥分发协议铺平了道路。