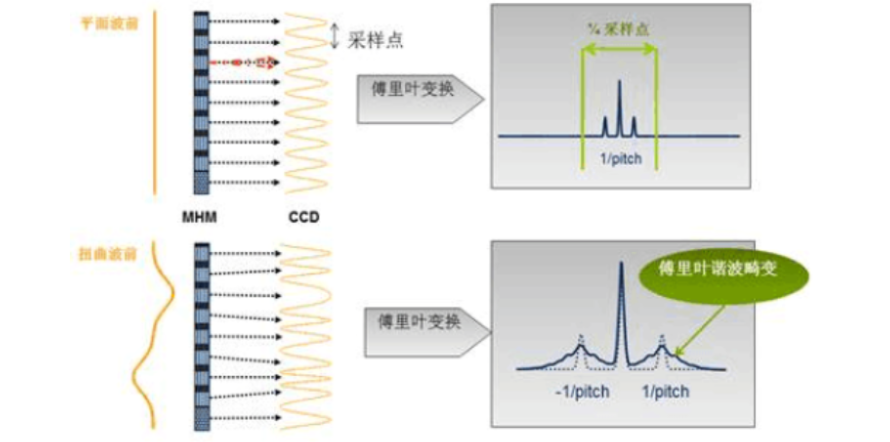
空间变化波前传感

空间变化波前传感

 

空间不变成像与

 

空间变化成像

01

 

光学成像技术在现代社会中扮演着重要角色，按照成像尺度可以粗略分为显微成像、摄影成像和天文成像，每种类别都有其独特的结构和功能。显微成像是一种利用显微镜或其他仪器将微米乃至亚微米的物体放大后观察其形态、结构和功能的技术，在生物学、医学、材料科学等领域发挥着重要作用，能够帮助人们揭示生命奥秘，诊断疾病，开发新材料等。摄影成像是一种利用相机或其他设备将光线反射或透射的图像记录下来的技术，在艺术、文化、教育、新闻等领域具有重要价值，能够帮助传播信息，记录历史，展示美感等。天文成像是一种利用望远镜或其他探测器将天空中的恒星、行星、星系等天体图像捕捉下来的技术。它在天文学、物理学、宇宙学等领域具有深远意义，能够帮助人们探索宇宙，理解自然规律，寻找外星生命信号等。

 

然而，在实际应用中，成像系统经常会受到像差的影响，导致图像模糊、失真和色散等现象，降低了图像对比度和清晰度。在图像上，这种现象常用点扩散函数（Point Spread Function，PSF）来表示，即当物平面上仅仅只有一个无限小的物发光时，成像系统拍摄的图像。无像差时PSF明亮而聚集，有像差时PSF暗淡且弥散。

如果增加一个特殊条件：这个无限小的点在物平面上不同位置上移动时，PSF仅仅发生平移，也就是说分布和形状不发生变化，那么这种成像系统被称为为空间不变系统（Space-invariant system），简称空不变系统，或我们称之为等晕系统。空不变系统可以用一个PSF表示其性质，并且成像过程直接利用卷积运算进行描述，不含像差和含像差的空不变成像模拟效果如图1所示。基于卷积模型，研究人员研发了大量的图像重建技术。

图1 无像差的理想成像与含像差的成像示意图，”⊗”表示卷积运算

 

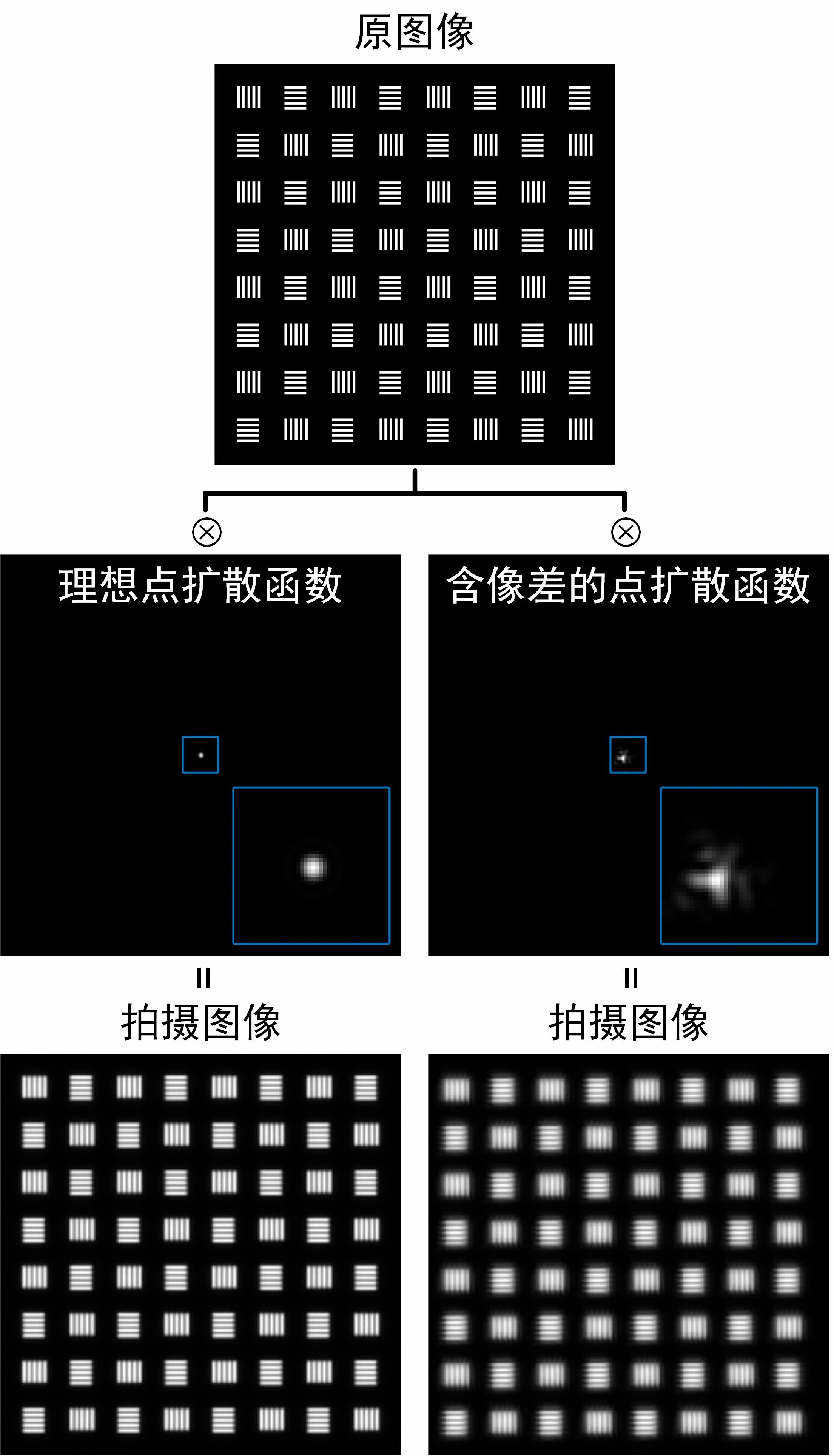
与空不变系统相对的，如果PSF随位置变化，则为空间变化系统（Space-variant system），简称空变系统，或我们称之为非等晕系统。空变系统理论上需要所有物点位置对应的PSF来描述，成像过程也不能通过卷积运算来描述，如图2所示，仅能描述为一般的线性过程，由于存在点点PSF分布差异，处理难度很大。

图2 空间变化条件成像示意图，”→”表示一般线性系统

 

对于空变系统成像，我们需要获取系统过程信息，打开这个黑盒，然后才有可能基于此设计合适的重建方法。如何获取系统过程信息便成为空变系统成像研究的重要部分，下面先介绍空不变系统下如何获得过程信息，然后介绍作者在此技术上如何拓展到空变成像系统。

02

 

空间不变波前传感与

 

Shack-Hartmann传感器

由前述可知，空不变系统过程信息可以用PSF来完整表示，进行PSF直接测量是一种常用的方法，这里给大家介绍另一个方法：波前传感器。如果说PSF是系统过程在像面的描述，那么在瞳面上则以波前来表述，其可以表示光行进的方向，如图3所示，一组波前与对应的PSF。波前有一个优势是其可以方便地计算PSF，但是从PSF想要获得波前需要特别的技术。

 

 

 

 

 

 

 

图3 波前与PSF

 

想要获得波前分布，最简单也是最常用的方法就是Shack-Hartmann波前传感器，它由一块微透镜阵列和相机组成，如图4所示。无扰动波前遇到Shack-Hartmann波前传感器，微透镜会将各区域的光分割后会聚到相机上，光统一朝向正前方，得到一张光斑阵列图，所有光斑都呆在微透镜的中心位置，如图4(a)中红色点阵；但当扰动波前达到微透镜阵列，各区域的光有各自的想法，在向前行进的过程中偏离“预定位置”，如图4(a)中蓝色；偏离大小与这个小局部的波前分布呈现一个简单线性关系，如图4(b)所示。就这样，拿到所有阵列中的偏移后，就能组合得到完整的波前分布。

 

图4 Shack-Hartmann传感器[1]及其原理示意图[2]

 

Shack-Hartmann

 

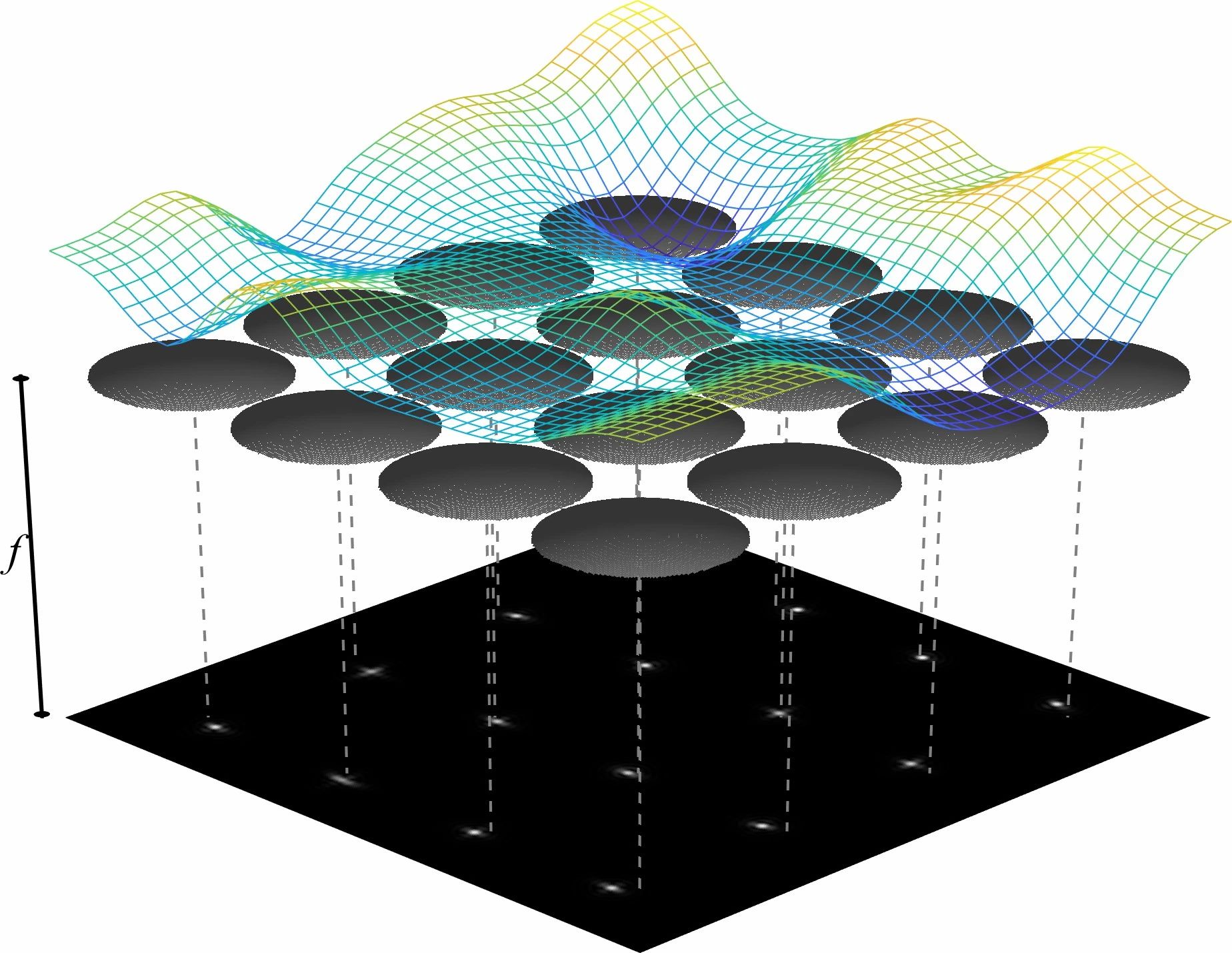
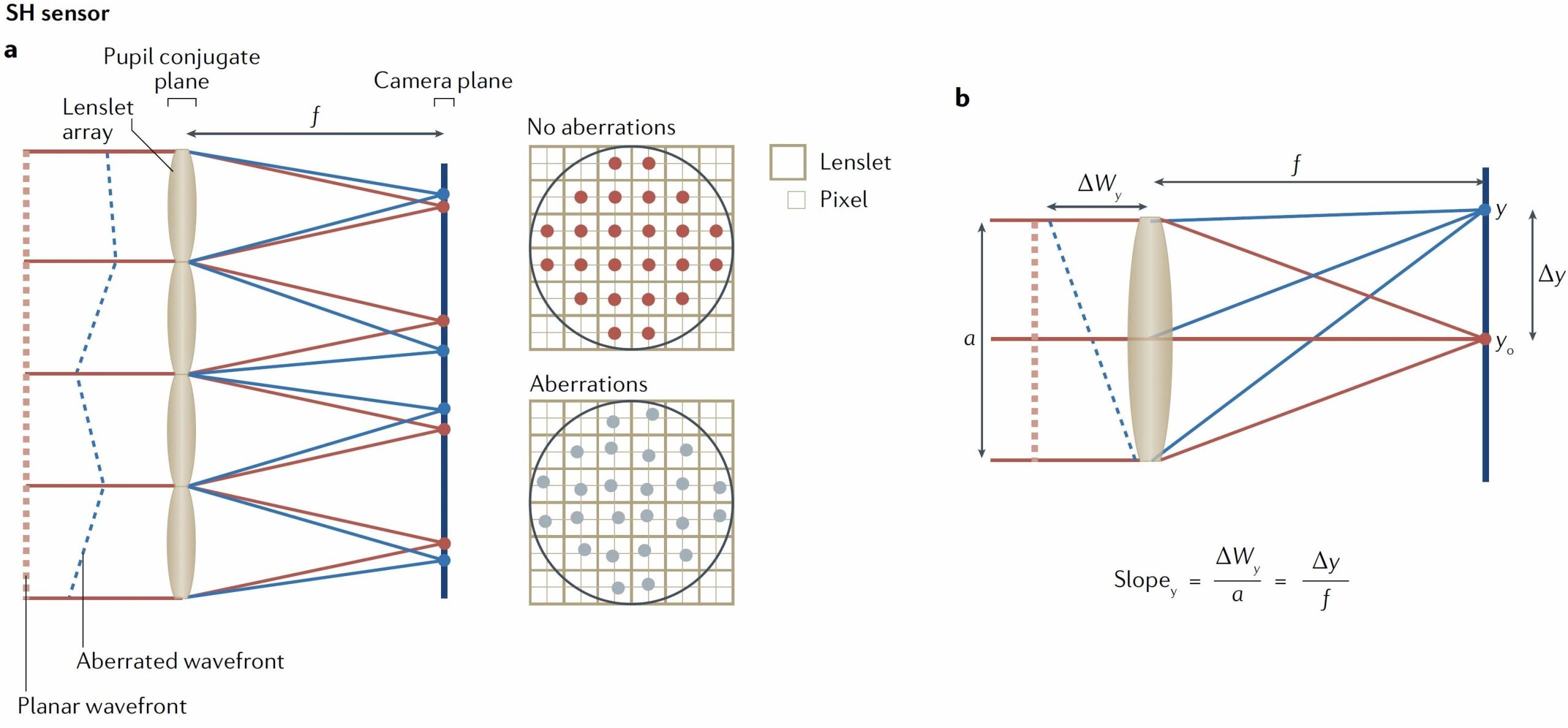
空间变化波前传感

03

 

如果将正入射的波前看作一个无穷远处光轴上的发光点，那么Shack-Hartmann传感器中任意一个微透镜后面的点斑就是这个点光源的像。如果“无穷远”处更换为扩展光源，微透镜后也将获得这个扩展光源的图像。在空间不变成像条件下，单个微透镜中扩展光源图像的偏移是一致的，如图5(a,b)所示；但在空间变化成像中，扩展光源各位置点走向并不一致，如图5(c)所示。在点光源照明条件下，可以通过计算质心位置来确定平移位矢（图5(a)）；而在扩展光源照明条件下，各位置点对应位矢不能直接用质心来求解，一般使用相关运算计算整体的平移位矢（图5(b)），我们提出使用图像配准算法计算位移场（图5(c)）。配准是一类计算机学科中根据两张或多张图像的信息分析图像相互变化的算法，配准算法会获得配准后的图像以及位移矢量场。配准算法多种多样，我们采用了基于图像结构相似度评分的优化算法，经过配准，也就获得了任意位置对应的位矢[3]。综合所有微透镜阵列的配准结果，我们就可以获得任意位置下的波前分布。至此，我们就得到了Shack-Hartmann空间变化波前传感框架。

图5 空间不变与空间变化条件下点光源与扩展光源照明的Shack-Hartmann波前传感示意图

 

04

 

基于光斑矩的

 

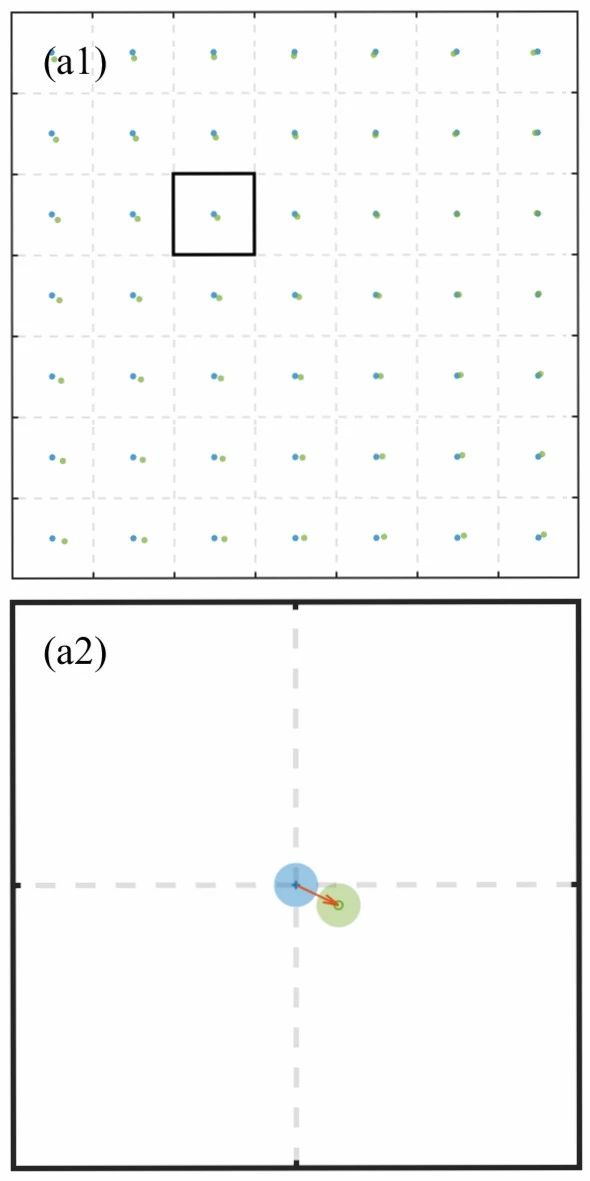
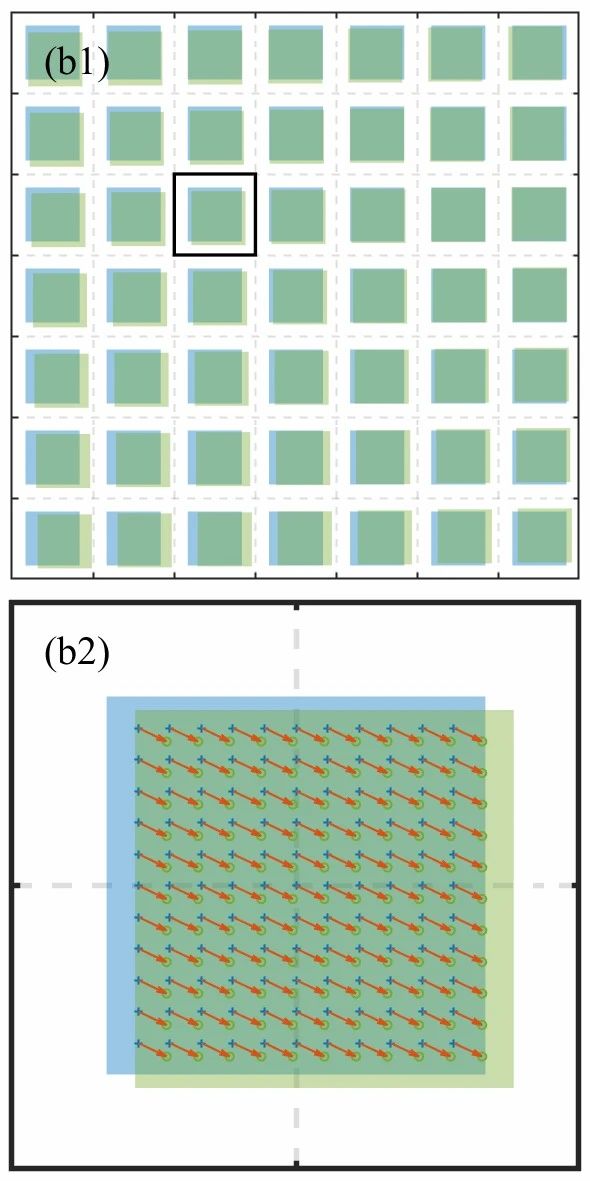
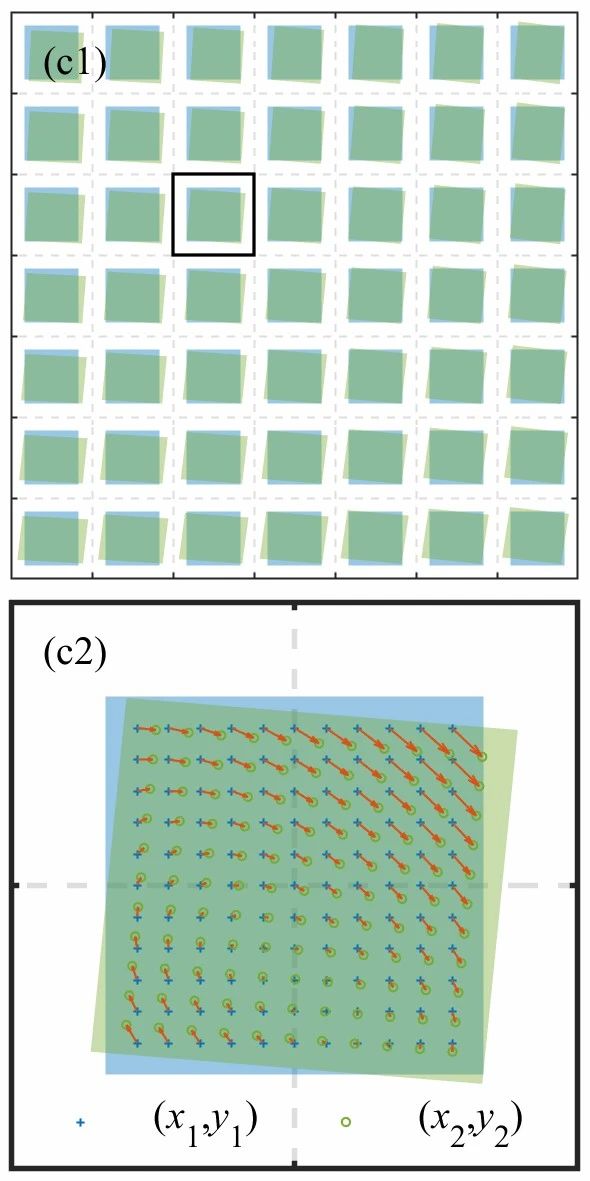
配准算法

除了采用通用配准算法，我们也设计了基于图像特征的直接计算配准算法。如图5(c)所示，图像形变不大的情况下，可以只用平移、旋转、缩放等基本图像变换来描述。平移有上、下两个自由度，旋转有一个旋转角度，缩放有上、下两个自由度，也就是说，需要求解5个未知的配准系数。我们知道，随机变量有均值和方差等数字特征，而图像也被认为是一个概率密度分布，均值、方差和协方差表示图像的位置、大小和方向，这些与更为高阶的数字特征统称为矩。自然而然，利用图像矩来计算配准系数就是一种不错的选择。我们推导两个图像矩与5个配准系数的关系，在正方形图像条件的帮助下，化简得到求解公式。基于光斑矩的配准算法计算速度比基于优化算法的快15倍，但是波前重建精度要低1/3[4]。

空间变化波前传感

 

与图像恢复

05

 

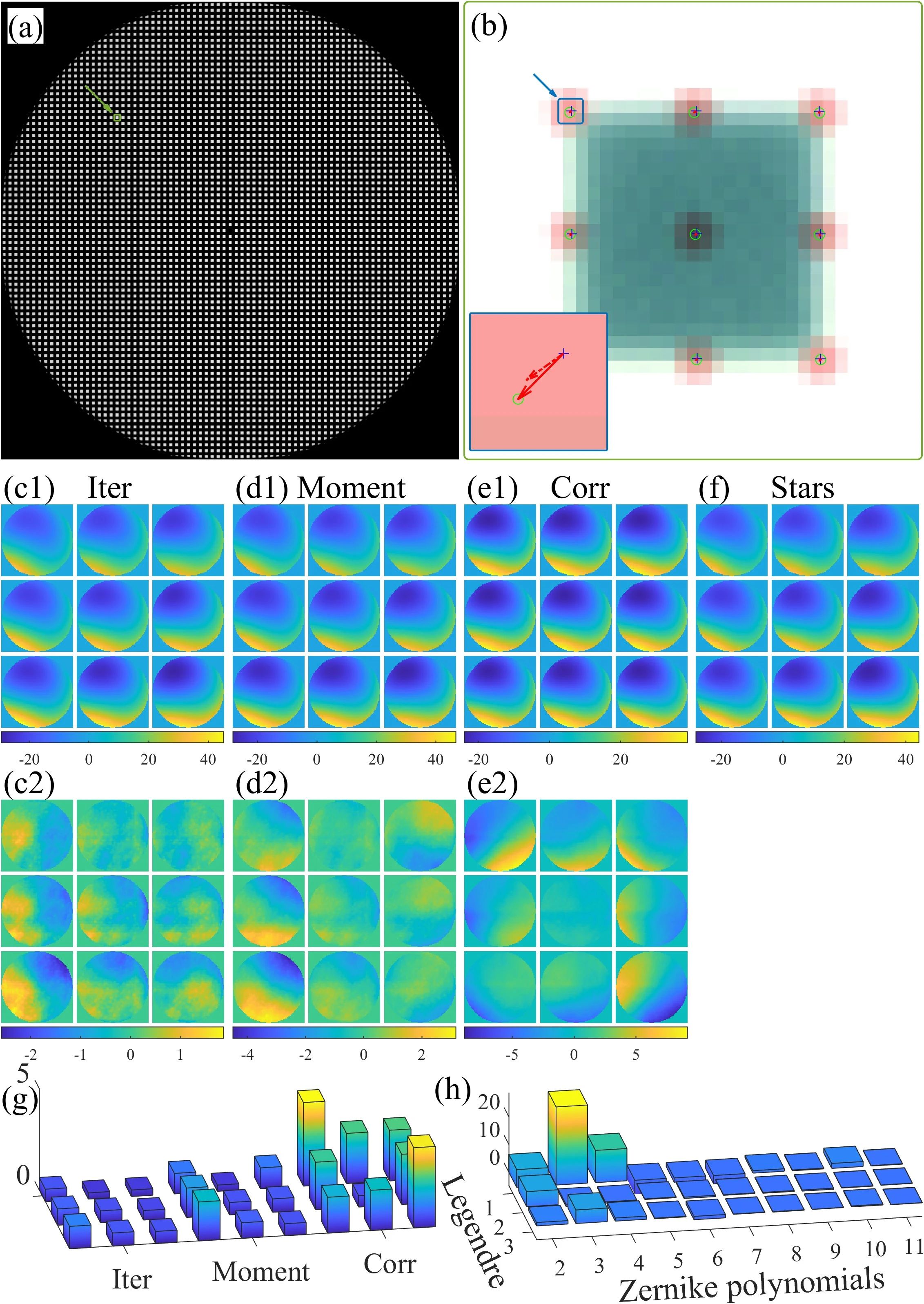
我们搭建了一个演示系统来验证上面的工作（图6），Shack-Hartmann传感器拍摄物镜后瞳分布（图7(a)），普通相机拍摄放大的图像（图8(a)）。使用前面介绍的两种方法，迭代优化（图7(c)）和矩（图7(d)），计算了9个位置的波前分布；通过对比常规质心算法（图7(f)）和相关算法（图7(e)），证实了该方法在空间变化波前传感的有效性和优越性。根据空间变化波前传感的结果，可以计算对应的PSF（图8(e)），对拍摄到的模糊图像各局部进行解卷积，最后组合获得最终恢复图像（图8(f)）。通过对比常规相关算法结果（图8(c,d)），验证了该方法在空间变化图像恢复的有效性和优越性。

图6 空间变化波前传感与图像恢复验证系统

 

图7 空间变化波前传感结果

 

图8 空间变化图像恢复结果

 

06

 

小结

 

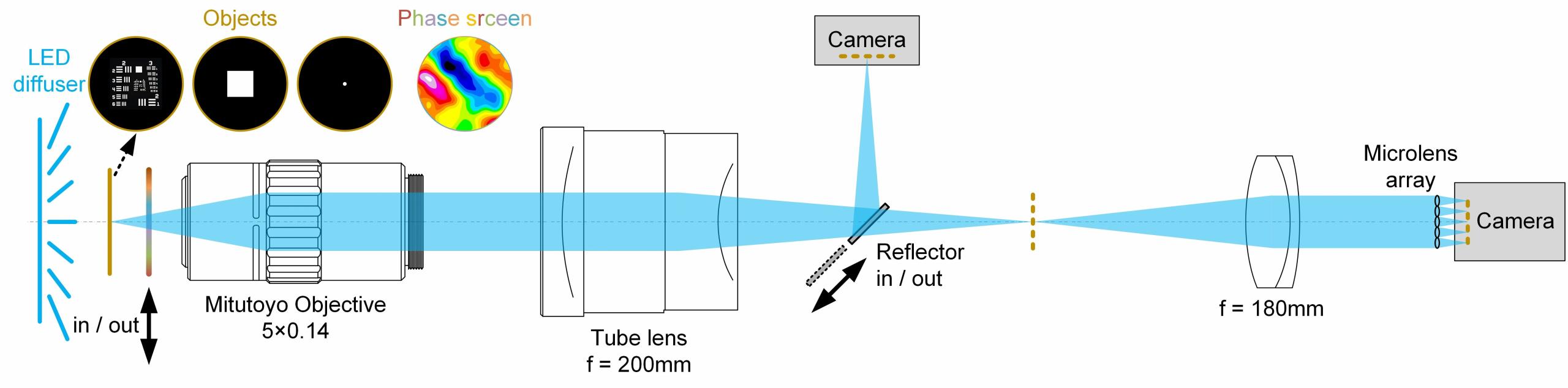
本文介绍了基于Shack-Hartmann传感器的空间变化波前传感框架，以及两种计算方法。基于优化的配准算法精度高、适应性强，基于光斑矩的算法速度快。空间变化成像是对空间不变成像的推广，可在超高分辨、超大视野、深层组织成像等领域发挥独特作用。

论文信息

 

⚪ Fan Feng, Chen Liang, Dongdong Chen, Ke Du, Runjia Yang, Chang Lu, Shumin Chen, Liangyi Chen, Louis Tao, and Heng Mao*, “Space-variant Shack–Hartmann wavefront sensing based on affine transformation estimation,” Applied Optics, 61, 9342-9349 (2022).

 

⚪ Fan Feng, Chen Liang, Dongdong Chen, Ke Du, Runjia Yang, Chang Lu, Shumin Chen, Wenting He, Pingyong Xu, Liangyi Chen, Louis Tao, Heng Mao, Moment-based space-variant Shack–Hartmann wavefront reconstruction, Optics Communications, 540, 129515 (2023).

参考文献

 

1. F. Feng, C. Li, and S. Zhang, “Moment-based wavefront reconstruction via a defocused Shack–Hartmann sensor,” Opt Eng 57, 074106 (2018).
2. K. M. Hampson, R. Turcotte, D. T. Miller, K. Kurokawa, J. R. Males, N. Ji, and M. J. Booth, “Adaptive optics for high-resolution imaging,” Nature Reviews Methods Primers 1, 68 (2021).
3. F. Feng, C. Liang, D. Chen, K. Du, R. Yang, C. Lu, S. Chen, L. Chen, L. Tao, and H. Mao, “Space-variant Shack-Hartmann wavefront sensing based on affine transformation estimation,” Applied optics 61, 9342-9349 (2022).
4. F. Feng, C. Liang, D. Chen, K. Du, R. Yang, C. Lu, S. Chen, W. He, P. Xu, L. Chen, L. Tao, and H. Mao, “Moment-based space-variant Shack–Hartmann wavefront reconstruction,” Opt. Commun. 540, 129515 (2023).

© 丰帆，All rights reserved.