基于E波段超表面的轨道角动量复用和解复用

Hyeongju Chung, Daeik Kim, Eunmi Choi and Jongwon Lee, E-band metasurface-based orbital angular momentum multiplexing and demultiplexing, Laser Photonics Rev. 16: 2100456 (2022).
轨道角动量模式是拉盖尔高斯模式的子集,由exp(ilφ)螺旋相位响应描述,其中方位角φ和方位角模式数l由2π相位变化的整数决定方位角方向。众所周知,具有不同模式编号的轨道角动量模式是相互正交的。这一特性理论上可以在单个频率上实现无限数量的正交通道,因此,可以通过自由空间或光纤创建承载数据的多个独立波束。多个正交轨道角动量模式可以与现有的集成多路复用技术,例如空分复用、波分复用和偏振分复用,为通信系统提供了额外的自由度。轨道角动量波束引起了广泛的兴趣,因为可能有一种新的通信系统可以应对当前数据容量呈指数增长的趋势。
使用轨道角动量波束的大容量自由空间通信需要用于多种轨道角动量模式的复用和解复用技术。特别是在射频和毫米波系统中的轨道角动量多路复用系统的情况下,诸如表面等离激元或均匀圆形天线阵列等结构用于轨道角动量波束生成和检测。最近,使用基于均匀圆形天线阵列的七种轨道角动量模式在40 GHz频带中200 m的距离处进行了117 Gbit/s无线传输。然而,在表面等离激元的情况下,系统复杂性很高且由于分束会产生额外的功率损耗。对于基于均匀圆形天线系统,很难集成额外的功能,例如波束成形。最近,研究人员开展了使用由超原子的二维排列组成的亚波长薄超表面生成和接收携带轨道角动量模式的涡旋光束的研究。超表面可以在组成超原子的单个水平上控制散射光的幅度、相位和偏振态。基于这些特性,各种平面光学元件和应用,如平面透镜、波片、全息图和轨道角动量光束发生器已被研究。为了产生基于超表面的轨道角动量光束,可以使用色散通过线性偏振入射光束下的超原子的结构尺寸控制或根据超原子的面内取向在几何相位下的几何相位来实现面内螺旋相位分布。使用这两种方法对超原子进行局部相位调谐不仅可以实现特定轨道角动量模式的螺旋相位分布,还可以实现各种类型的光束操纵,例如光束聚焦和转向。因此,根据相位分布和远场模式的傅里叶变换关系,通过将相应的二维相位分布相乘,可以将波前工程的多种功能同时集成到一个超表面中。在之前的研究中,研究人员实现了E波段频率的超表面,它集成了螺旋相位图案以创建轨道角动量模式,用于光束转向以减少干涉的梯度相位图案以及透镜相位图案以减少轨道角动量光束的发散角。最近,理论上提出了使用单个超表面的自由空间轨道角动量复用和解复用方法并通过显示轨道角动量模式转换的场分布在太赫兹区域进行了实验证明。然而,实验研究并未提供轨道角动量复用的信噪比,而是对E波段频率进行了研究,该频率是未来超高密度前传和后传可用的6G无线通信频段运输网络,尚未报告。
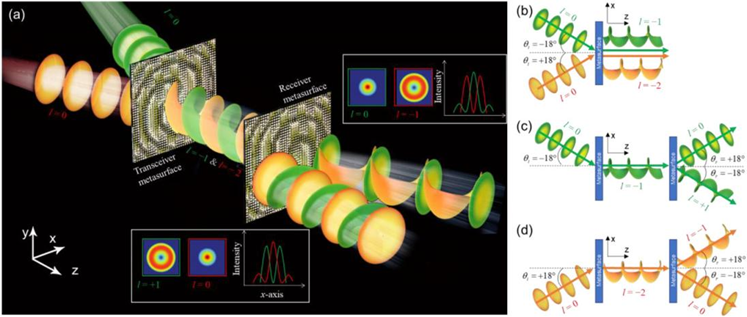
图1 a,基于一对具有相同设计的超表面的轨道角动量复用和解复用示意图。绿色和橙色代表两种不同的数据承载光束。在通过收发器和接收器超表面后,两个入射高斯光束携带的数据使用在两个离轴方向上形成的高斯光束接收。b,通过收发器超表面分别从入射角为-18°和+18°的高斯光束生成l = -1和-2的轨道角动量光束的示意图。c,d,入射高斯光束通过收发器和接收器超表面的入射角为-18°(c)和+18°(d)的光束变换示意图。
图1a显示了基于超表面的轨道角动量复用和解复用操作的示意图。具有不同入射角的两个高斯光束通过前收发器超表面转换为l=-1和-2的同轴轨道角动量光束(图1b),然后,通过两个折射角方向将其转换为不同的轨道角动量模式后接收器超表面。在这种配置中,进入接收器超表面的轨道角动量l=-1分别在+18°和-18°的折射角处形成高斯光束和轨道角动量光束l=+1(图1c)。类似地,进入接收器超表面的轨道角动量l=-2形成轨道角动量光束l=-1和折射角分别为+18°和-18°的高斯光束(图1d)。在这里,入射角和折射角由图1a-d中设置的坐标中的x方向波矢量的符号确定。因此,通过接收器超表面的光束在两个折射角方向上形成同轴轨道角动量和高斯光束并在光束中心产生很大的强度差异(1a中的白框)。
为了构建这样的超表面,研究人员首先基于传递矩阵方法设计了具有高传输效率和2π相位覆盖的元原子单元结构。在超原子设计中,多层参考使用具有不同厚度(分别为dA和dB)和有效介电常数以A-B-A形式堆叠的A层和B层的结构,如图2a所示。对于在dA=0.468 mm和dB=0.35 mm处具有固定厚度的每一层,通过传递矩阵方法在频率为83 GHz,结果分别如图2b和c所示。在这个计算中,研究人员假设这两层是无损的。从透射率和透射相位的图中,可以提取出具有高透射率的超原子结构和构成超表面的特定透射相位值所需的两个介电常数。为了构建超表面,研究人员提取了八组不同的ABA 结构介电常数。然后,基于这些值设计了八种不同的超原子结构。具有三种不同材料的间原子结构的横截面示意图,如图2d所示。A层由铜天线、介电基板(RF-35A2,介电常数为3.5,损耗角正切为0.0018)和键合膜(DS-7409DV(N),介电常数为3.3,损耗角正切0.003)组成。B层由相同的基板、铜天线和相同的接合膜构成。超原子结构的总厚度为 1.286 mm,比工作波长(λ=3.61 mm,83 GHz)小三倍。对于超原子结构,A层和B层所需的有效介电常数是通过调整位于每层中的偶极子或网状铜天线的结构来获得的。研究人员获得八种不同的元原子结构所需的层A和B的天线结构,如图2e所示。图2f显示了x偏振入射光束下八个超原子结构的透射率和透射相位的模拟结果,如图2e中的轴所示。使用图2b、c中绿点表示的这八个元原子结构,可以以45°的间隔覆盖2π相位且在83 GHz 下获得超过65%的透射率。应该注意的是,由于材料损失,八种设计的超原子结构的有效介电常数在通过传递矩阵方法的相位图中没有显示出精确的45°相位差。
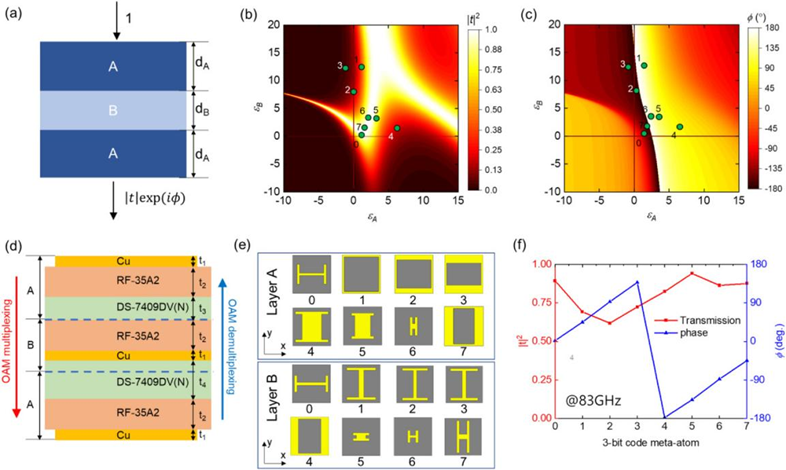
图2 a,基于传输矩阵方法的超原子设计具有固定厚度 dA=0.468 mm和dB=0.35 mm的ABA多层结构。b,c,ABA结构的计算透射率 (b)和透射相位 (c)作为层A和B的有效介电常数的函数。绿点代表为设计八种不同的超原子结构而提取的有效介电常数值。d,由基板 (RF-35A2)、粘合层 (DS-7409DV(N)) 和铜天线层构成的 ABA多层结构的横截面示意图。厚度为t1=0.018 mm、t2=0.25 mm、t3=0.1 mm和 t4=0.3 mm。e,用于八种不同超原子结构的层 A(顶板)和 B(底板)的铜天线结构。f,八种不同的间原子结构在83 GHz频率下的模拟透射率(左轴)和传输相位(右轴)。
对于具有离轴积分的l=-1和-2的轨道角动量模式的复用和解复用,超表面的传输函数由等式描述:
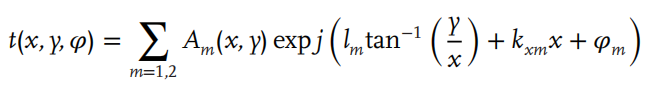
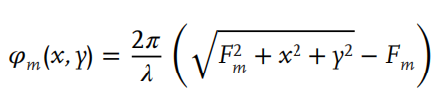
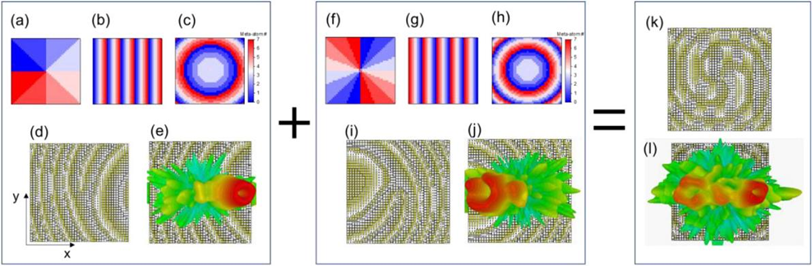
图3 a,轨道角动量模式 l=-1代的螺旋相位模式。b,用于在+x方向引入附加波矢量的一维相位梯度模式。c,F=150 mm的透镜相位图。d,设计的超表面整合(a-c)中的相位模式。e,在高斯光束的法向入射下,从(d)中的超表面生成的轨道角动量光束的模拟远场图案。f,轨道角动量模式 l=-2代的螺旋相位模式。g,用于在-x方向上引入额外波矢量的一维相位梯度模式。h,F=100 mm的透镜相位图。i,设计的超表面整合(f-h)中的相位模式。j,在高斯光束的法向入射下,从(i)中的超表面生成的轨道角动量光束的模拟远场图案。k,整合(d)和(i)中的两个相位模式的超表面图像,用于同时生成轨道角动量模式l=-1和-2。l,在高斯光束的法向入射下,生成的轨道角动量光束的模拟远场图案,在+x方向上 l=-1,在-x方向上 l=-2。
为了实验实现,研究人员使用标准印刷电路板工艺制造了超表面。图4a显示了制造的超表面的照片。超表面的尺寸为201×201 mm2 (55.68×55.68λ2)。图4b显示了测量设置。锥形喇叭天线产生波束半径为8 mm的水平极化高斯波束。图4c显示了使用入射角为+18°的高斯输入光束生成轨道角动量模式l=-2的测量顶视图。然后,轨道角动量模式l=-2以+18°的折射角转换为高斯光束。喇叭天线和收发器超表面、收发器和接收器超表面以及接收器和矩形波导探头之间的距离分别为 100 mm、200 mm和150 mm。通过以1 mm的步长在x和y方向扫描来自收发器和接收器超表面的传输光束,使用矢量网络分析仪的两个端口测量100×100 mm2 区域中Ex场的2D分布。
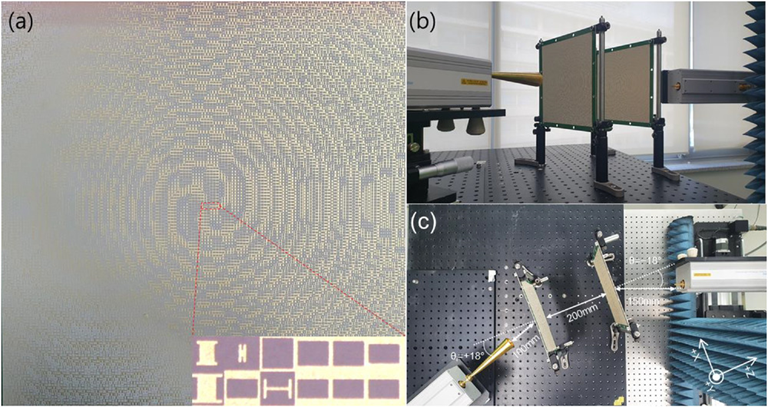
图4 a,处理后的超表面的顶视图和超表面中心区域的单位结构图像的(插图)放大视图。b,测量装置的侧视图。c,通过收发器超表面(左)产生 l=-2和通过接收器超表面(右)接收高斯光束的轨道角动量光束的测量设置的顶视图。
Ex场的归一化强度和相位分布的模拟和实验结果,如图5所示。图5a-d显示了轨道角动量光束的模拟和测量的Ex场分布,其中l=-1和-2收发器生成入射高斯光束的超表面,角度分别为-18°和+18°。生成的轨道角动量光束在z方向上传播,场分布在距超表面150毫米处进行监测。Ex场强和相位分布的测量结果与模拟结果吻合良好。图5e-h显示了当l=-1的轨道角动量光束垂直于接收器超表面入射时,转换和透射输出光束的Ex场强度和相位分布的模拟和测量结果。输出光束在+18°的折射角方向分裂,形成轨道角动量模数+1添加的高斯光束,在-18°的折射角方向,形成l=1的轨道角动量光束+1由轨道角动量模式编号+2添加。类似地,当l=-2的轨道角动量光束入射到接收器超表面时,转换和传输的输出光束在+18°和-18°的转向角方向上分裂,形成l=-1和高斯光束,如图5i-l所示。结果还表明模拟和实验之间的一致性很好。此外,研究人员进行了Ex场的轨道角动量模式纯度分析。图5中白色虚线的圆形区域表示生成的轨道角动量模式的主要强度。大多数模拟和测量结果的轨道角动量模式纯度都超过80%,但实验测量中存在一些偏差,因此,模式纯度达到69%。
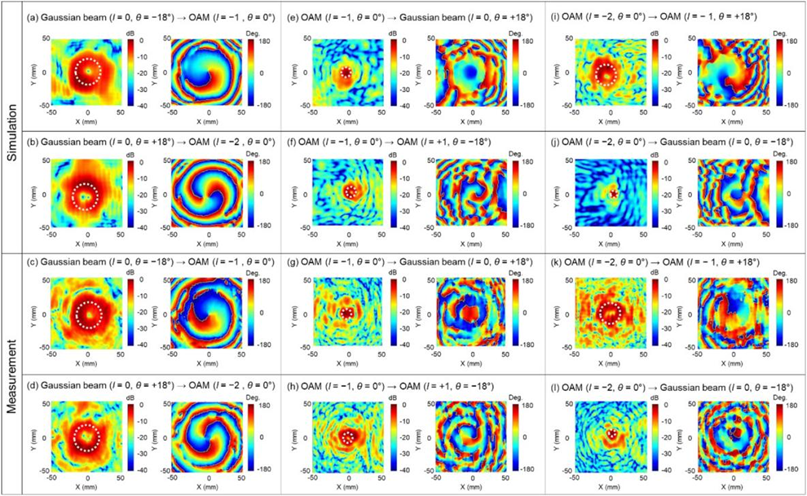
图5 a-d,生成的轨道角动量光束的Ex场的归一化强度(左)和相位(右)分布的模拟(a,b)和测量(c,d),其中,l=-1(a,c)和 图2(b,d)来自输入高斯光束下的收发器超表面,入射角为-18°(a,c)和+18°(b,d)。e-h,折射角为+18°的生成的高斯光束 (e,g) 的Ex场的归一化强度 (左) 和相位 (右) 分布的模拟 (e, f) 和测量 (g, h) °和轨道角动量光束l=+1(f,h),在具有l=-1的轨道角动量光束的法向入射下,从接收器超表面的折射角为-18°。i-l,生成的轨道角动量光束的Ex场的归一化强度 (左) 和相位 (右) 分布的模拟 (i,j) 和测量 (k,l),其中,l=-1 (i,k),a在具有 l=-2的轨道角动量光束的法向入射下,折射角为+18°和高斯光束(j,l),从接收器超表面折射角为-18°。白色虚线圆线表示轨道角动量模式的主要强度。
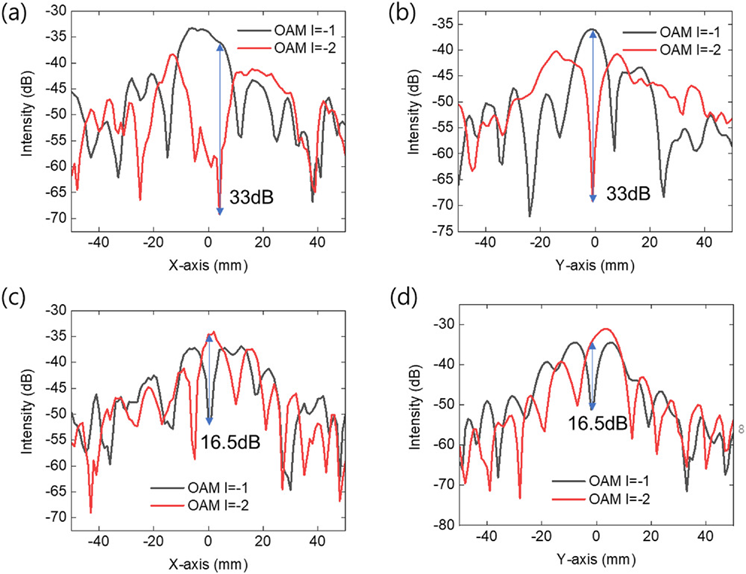
图6 a-d,在 x- (a, c) 和 y 轴上扫描l= -1 (黑色) 和-2(红色)的入射 轨道角动量光束的接收器超表面的输出光束的测量Ex场强度分布沿+18°(a,b)和-18°(c,d)的折射角方向的横向平面的(b,d)。蓝色双边箭头分别表示33 dB(a,b)和16.5 dB(c,d)的光束强度差异。
如表1所示,以前大多数基于超表面的轨道角动量多路复用研究仅显示了转换后的轨道角动量模式场分布。特别是在微波区域,由于使用VNA扫描电场,因此存在检测轨道角动量模式需要较长时间的问题。为了克服这个问题,研究人员提出了一种方法,该方法可以通过将检测器定位在转换后的轨道角动量和通过接收器超表面的高斯光束的中心,利用强度差异立即检测轨道角动量模式。在离轴传播方向上,通过接收器超曲面进行转换和转向的轨道角动量光束在横截面中心具有最小强度值,而通过接收器超表面进行转换和转向的高斯光束在中心具有最大强度值离轴传播方向的横截面。因此,使用在光束中心获得的最大强度对比度,可以检测和识别用于自由空间通信的传入轨道角动量光束。图6显示了在+18°(图 6a,b)和-18°(图 6c,d)的折射角形成的高斯和轨道角动量光束的横向平面中沿x和y轴扫描的强度分布结果。如图 6a、b 所示,获得33 dB的光束强度差异来检测和识别l=-1进入接收器超表面的轨道角动量光束。在具有l=-2的轨道角动量光束进入接收器超表面的情况下,如图 6c、d 所示,获得了16.5 dB的强度差异。
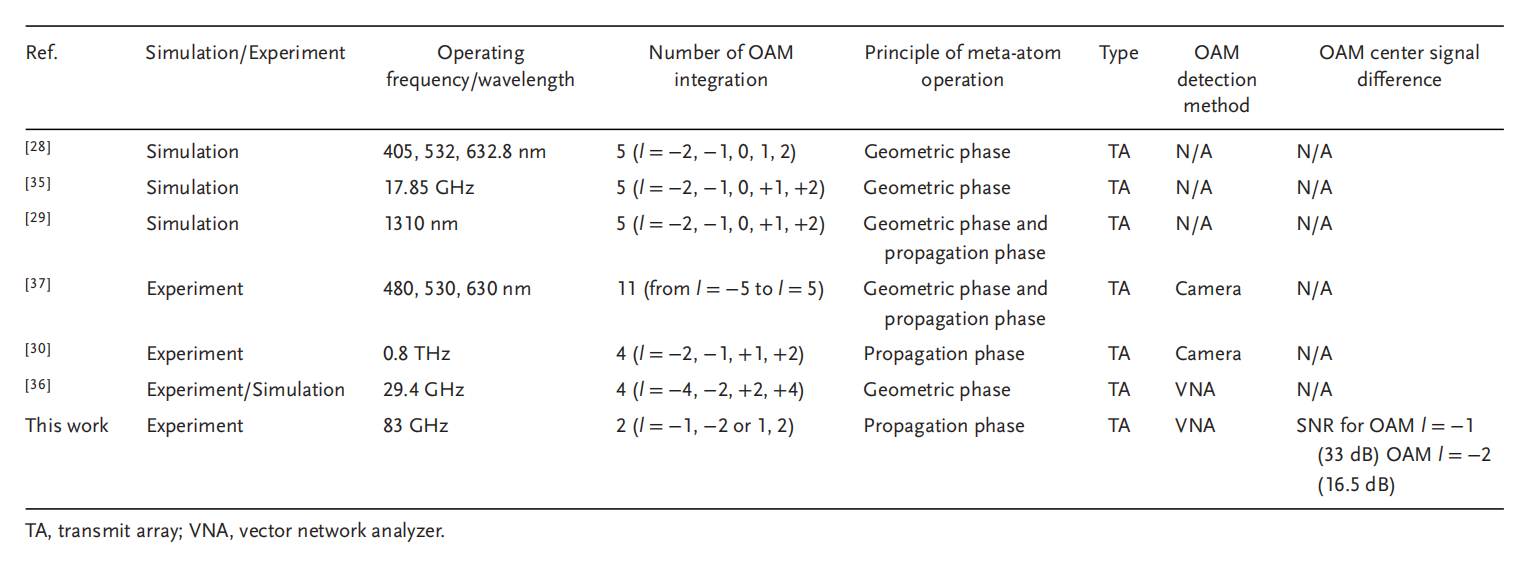
表1 基于超表面的OAM多路复用的工作复用和解复用的性质比较。
综上所述,研究人员提出并通过实验实现了使用一对相同结构的超表面进行轨道角动量复用和解复用。两个离轴高斯光束通过具有集成轨道角动量模式生成、光束控制和聚焦特性的收发器超表面转换为l=-1和-2的轨道角动量光束。通过为通过接收器超表面的两个离轴方向添加轨道角动量模式编号+1和+2,来控制和转换生成的轨道角动量光束。在这种配置中,每个轨道角动量波束所携带的信息都可以通过位于输出波束横向平面中心的点检测天线探头来接收。对于概念验证演示,仅考虑了离轴光束和 x 轴方向的转向,但在非x轴方向上进一步分裂可以进一步增加轨道角动量光束的通道。值得注意的是,大多数基于超表面的轨道角动量多路复用研究都表明了空间分布的轨道角动量光束轮廓。然而,对于实际自由空间通信,需要使用最少数量的接收天线探头来构建系统。这项研究中提出的轨道角动量复用和解复用方法在这方面提供了最现实的替代方案,相信它将为自由空间轨道角动量通信提供有效的设计方法。
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。