Menu 

Menu
  1. 首页
  2. 行业新闻
  3. Holo-Encoder: 自编码器网络实现全息图快速生成 (OSA OL)

Holo-Encoder: 自编码器网络实现全息图快速生成 (OSA OL)

Holo-Encoder: 自编码器网络实现全息图快速生成

High-speed computer-generated holography using an autoencoder-based deep neural neTWork

本期导读

空间光调制器（SLM）和超表面能够对光波的振幅或相位进行调控，实现所需的光场分布，在光束整形、光场调控和全息显示等领域有着重要应用。纯相位全息图可以用于产生各种所需的光场。为了生成纯相位全息图，计算全息（CGH）技术受到了广泛的关注。
    目前，传统的迭代优化方法需要在算法运行时间和重建光场质量之间进行折衷，无法满足实时和高质量显示的需求。随着计算机性能的提高和深度学习技术的发展，如何快速高效地生成相位全息图成为近年来的研究热点。日前，来自清华大学的研究人员提出了一种自编码器网络，可以实现计算全息图的快速生成，该成果近期发表在OSA经典期刊《Optics Letters》上。

Image

研究背景

纯相位全息图的计算是一个不适定（ill-posed）问题。对于给定的光场分布，相应的纯相位全息图是否存在，以及全息图是否唯一都是不确定的。传统计算全息可分为迭代和非迭代两大类。迭代方法利用优化算法，寻找符合条件的最优全息图，如Gerchberg-Saxton (G-S)算法，Wirtinger算法等。这类方法图像重建质量随迭代次数增加而提高，要想实现高质量全息图，需耗费大量计算时间。为了实现快速CGH，学术界提出了几种非迭代方法，如空间复用、误差扩散和相位编码等。然而这些方法以牺牲空间分辨率为代价实现复振幅调制，并且容易在重建图像中出现伪影。
近年来，深度学习以其灵活高效的性能成为解决这类具有挑战性问题的有力工具。基于深度学习的CGH方法可以同时提供高速和高质量的图像重建，实现实时动态地光场调控和显示。通常来说，基于学习的方法需要事先生成全息图作为神经网络的训练集，不适合大规模数据集的生成。而无监督学习无需对应的标记数据集，网络性能不受标记数据集的质量，是一种适合基于学习的CGH方法的训练方法。

Image

技术路线

       该研究提出了一种基于自编码器结构的神经网络用于生成计算全息图。称之为全息编码器（Holo-Encoder）。自编码器是一种无监督神经网络，最初用于学习如何有效地压缩和编码数据。其输入和学习目标均为相同图像，网络结构分为编码部分和解码部分，连接编码和解码部分的隐藏层在训练结束后输出编码图像。由于全息图的记录和重建可以看作是图像的编码和解码，因此全息显示的图像端到显示端的计算模型可以用一个自编码器来表示。自编码器输入为原始图像，输出为重建图像，中间的隐藏层代表对应的全息图。该方法不需要图像对作为数据集，只需要一个图像数据集即可，可以大大节省图像的采集时间成本。

与一般自编码器有所不同，全息图的解码是一个确定的衍射传播模型。全息编码器通过将物理模型融入到网络的训练中，既可以实现对目标图像的全息图的优化，又可以学习目标图像到全息图的映射。

Image

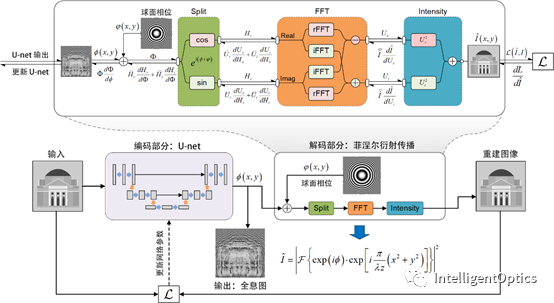
图 1  Holo-encoder网络结构示意图

全息编码器的编码部分采用U-Net结构，由四个下采样模块和四个上采样模块构成。每个模块由两组批处理归一化、非线性激活层（ReLU）和卷积层组成。U-Net的输出层是一个tanh函数，它将相位值限制在[-π，π]范围内。
全息编码器的解码部分属于无学习参数的衍射传播模型。网络中采用菲涅耳变换方法，只需要一个傅里叶变换，且不需要补零操作，节省了大量的计算资源。为了处理神经网络中复数的反向传播，首先利用欧拉公式将相位分解为复振幅的实部和虚部，然后将傅里叶变换分解为实部rFFT和虚部iFFT的两个单独的变换，最后重建的强度为实部和虚部的平方和。
网络的训练采用负皮尔逊相关系数（NPCC）和感知损失组合来构造损失函数。还可选择全变差正则化对重建光场相位施加约束，使相位变化更为平滑，从而减少重建图像的散斑噪声。借助神经网络的自动微分，损失函数的误差能够反向传播到编码部分，并在训练过程中更新U-net的参数。

Image

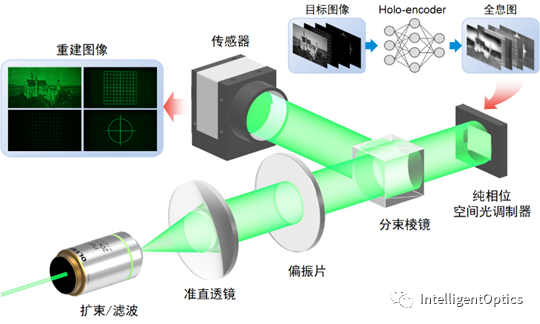
图 2  基于holo-encoder的全息显示光路图

泛化能力是评价神经网络性能的重要依据。该实验利用不同于训练集类型的数据来测试所提网络的可泛化性，包括方形网格、激光点阵、十字三种二值图案。Holo-Encoder可以快速计算出任意目标图案的全息图（图3），当采用激光照明全息图时，就可以在一定距离上得到准确的目标图案。这充分展示了全息编码器具有较强的泛化能力，在衍射光学元件的设计中具有很大的潜力。

Image

图 3  Holo-encoder编码二值图像全息图和重建结果

对于灰度图像而言，重建光场中的相位扰动会导致散斑的产生，在损失函数中引入了重建相位的正则化项，全息编码器可以产生更平滑的相位分布，重建图像具有更少的散斑（图4）。由Holo-Encoder产生的全息图和迭代方法产生的全息图的分布相比，更加抽象和分散，但它们投影所产生的图案效果是一样的。

Image

图 4  三种CGH方法结果比较

    基于学习的计算全息技术为全息显示提供了一种快速的全息生成方法。本文提出一种基于自编码器的神经网络，全息编码器用于纯相位全息图的生成。全息编码器通过将物理模型融入到网络的训练中，可以在无监督的情况下自动学习纯相位全息图的编码。该全息编码器能够在0.15秒内生成高保真4K分辨率的全息图。
    另一方面，该方案目前亦存在一些问题，如何考量更加具有实际物理意义的模型而非简单地使用单一Unet作为phase encoder，同时进一步提升图像质量和处理速度。如能进一步完善，相信该方法将适用于实时三维显示、增强现实显示。同时也期待该方法可以促进光场操纵在生物医学科学和工业中的应用，例如全息多光子显微镜和衍射光学元件的设计。

论文信息：

Jiachen Wu, Kexuan Liu, Xiaomeng Sui, and Liangcai Cao, “High-speed computer-generated holography using an autoencoder-based deep neural network,” Optics Letters 46, 2908-2911 (2021).

技术详见：

https://github.com/THUHoloLab/Holo-encoder

*该技术分享所涉及文字及图片源于作者J.C. Wu提供及网络公开素材,不做任何商业用途。

本文注明来源为其他媒体或网站的文/图等稿件均为转载，如涉及版权等问题，请作者在20个工作日之内联系我们，我们将协调给予处理。最终解释权归旭为光电所有。

高速三维测量，让稍纵不再即逝高速三维测量，让稍纵不再即逝 深度学习赋能下的光学计量：让“老司机”搭上“顺风车”深度学习赋能下的光学计量：让“老司机”搭上“顺风车” 12张封面带你回顾Chinese Optics Letters的202212张封面带你回顾Chinese Optics Letters的2022 超快成像：基于复数神经网络重构实空间复杂结构超快成像：基于复数神经网络重构实空间复杂结构 “虚拟”的平面，加速生成计算全息图“虚拟”的平面，加速生成计算全息图 Layertec超快激光反射镜Layertec超快激光反射镜 衍射模型驱动的无监督层析计算全息 (Optica OE)衍射模型驱动的无监督层析计算全息 (Optica OE)