光学涡旋晶格：对轨道角动量的开发

1974年，Ney和Berry发现了波列中的位错，激发了人们对相位奇点和光学涡旋的兴趣。1992年，Allen等人发现光子具有轨道角动量，这为光子提供了额外的自由度。光学涡旋具有螺旋相位exp(jmθ)和轨道角动量mħ，其中，m是拓扑荷，θ是角坐标。光学涡旋具有许多应用，包括光学成像、光镊的生产和光学通信。为了满足多种应用的要求，研究人员研究了包含多个单位涡旋的光学涡旋晶格。通常，光学涡旋晶格通过叠加光学涡旋生成，并带有镶嵌在光环上的光学涡旋。

作为一个典型的光学涡旋晶格，2007年，光学摩天轮光场通过两个拉盖尔-高斯光束与特定拓扑荷对的叠加产生。它可以适当地捕获冷原子和量子简并原子样品。2009年，该束成功应用于捕获单个铷原子。同年，研究人员基于该光束提出了一种交流驱动的原子量子电机。为自由调制光学涡旋晶格模式，研究人员通过两个同心完美光学涡旋的叠加产生了圆形光学涡旋晶格。此外，光学涡旋晶格被操纵成多功能结构。然而，光学涡旋晶格的暗核在原子操纵中几乎没有被利用。光学涡旋晶格中光学涡旋上轨道角动量的物理量似乎被忽略了。这是为什么？答案隐藏在轨道角动量的数量中。单位光学涡旋上的拓扑荷总是±1，产生的轨道角动量可以忽略不计。因此，在光学涡旋晶格中产生“扳手力”的轨道角动量尚未被利用。相反，微小物体的捕获和旋转在一些先进的应用中是必不可少的，例如，在光驱动电机、DNA旋转检测、流体力学和细胞分选中。

因此，应利用轨道角动量，开发具有高阶拓扑荷的光学涡旋晶格。为了应对这一挑战，2013年，Chen等人研究了一种具有高阶轨道角动量的光学涡旋晶格，其通过特定的拉盖尔-高斯模式产生。然而，光学涡旋的数量与其阶数有关，从而导致光学涡旋晶格模式的未调制。此外，2018年，研究人员修改了这种方法，通过使用几个加权因子来获得任意高阶光学涡旋晶格。值得注意的是，在这种方法中，幂指数应用于拉盖尔-高斯光束的复振幅，限制了特定应用的模式调制。这些工作激励人们将光的复振幅分离为振幅和相位项，然后进行调制。

为了产生模式可控的高阶光学涡旋晶格，研究人员将两个光学涡旋光束成形为所需的任意结构。接下来，通过这些可变形光学涡旋光束的叠加来构建光学涡旋晶格。理论上，将光学涡旋晶格的复振幅分为振幅项和相位项。提取并调制相位项以获得高阶拓扑荷。随后，调制相位乘以振幅项以重建光学涡旋晶格的新的复振幅，即高阶光学涡旋晶格。

此外，光学涡旋晶格中单位光学涡旋的高阶拓扑荷的产生至关重要。因此，必须解释清光学涡旋晶格中光学涡旋总是±1的原因。圆上奇点的数量可以推导出来。这里试图回答这个问题：“为什么光学涡旋晶格中单位光学涡旋的拓扑荷总是±1？”例如，图1(a1)和(b1)显示了具有拓扑荷分别为1和3。为了便于分析，研究人员将相位环横向展开为矩形，并在限制条件下离散为一个序列。图1(a1)中所示的相位被离散为从a_q开始并具有q项的等差序列[图1(a2)]，其中，a₁=0，a_q=2π。类似地，图1(b1)中所示的相位被离散为三个算术序列，从b₁开始，具有p项[图1(b2)]，其中，b₁=0，b_p=2π。注意，在图1(a2)和(b2)之间，每个项的大小相等。在这种情况下，p=q/3，即两个光学涡旋光束完全重叠，干涉瓣出现在没有单位光学涡旋的情况下。然后，研究人员考虑两个光学涡旋光束部分重叠。首先，图1(a1)所示的相位是叠加的外圈。在这种情况下，内环的离散项数量仅比外环少一个，即p=(q−1)/3，结果如图1(c)所示。叠加区只有4对0和2π项。同时，每个奇点周围只有一个周期从0逆时针增加到2π。根据方程中拓扑荷的定义，光学涡旋晶格中单位光学涡旋的拓扑荷总是−1。此后，将图1(b1)中所示的相交换为叠置的外环。类似地，在这种情况下，p=(q+1)/3且在相位从0顺时针增加到2π的位置附近产生了四个正单位光学涡旋（拓扑荷=+1）[图1(d)]。一般来说，考虑到不同的叠加光学涡旋光束，唯一的变化是光学涡旋晶格中单位光学涡旋的数量和符号。此外，从先前的参考文献中获得的每个光学涡旋的拓扑荷的大小保持不变。因此，应在叠加相位上执行附加操作，以从光学涡旋晶格获得高阶光学涡旋。

 

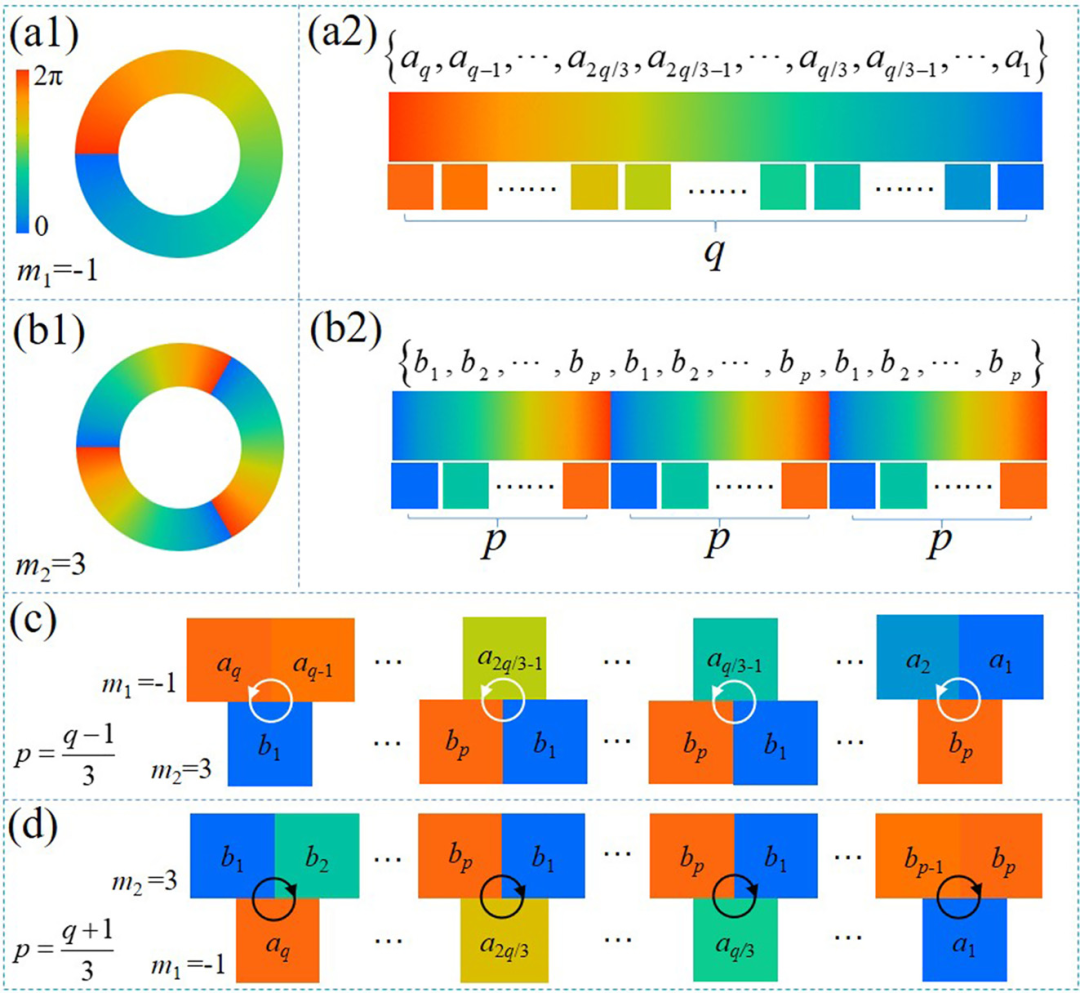
图1 光学涡旋晶格中单位光学涡旋的拓扑荷始终为±1的示意图。（a1）和（b1）光学涡旋光束的拓扑荷分别为-1和3。（a2）和（b2）水平展开和离散算术序列。（c）和（d）两种不同情况下的叠加，白色和黑色圆圈箭头分别表示负和正单位光学涡旋。

值得注意的是，指数函数exp[jψ₀(s)]是一个周期函数，它将相位截断为几个周期，0-2π。因此，在光学涡旋晶格中可以获得光学涡旋的高阶拓扑荷。图1显示了原理示意图。其中，光学涡旋晶格中光学涡旋的拓扑荷乘以3。上排是一个单位光学涡旋的乘法过程的三维表示。中间和下部行分别表示光学涡旋晶格的相位重建和特定光学涡旋的放大。

高阶光学涡旋晶格表现出圆形结构中光学涡旋的调制。高阶光学涡旋晶格只展示了圆环形结构的调制。然而，为了在多微粒子操纵中充分发挥轨道角动量的作用，高阶光学涡旋晶格模式应该可以被任意调制。为了实现这一点，光学涡旋光束的结构在叠加之前通过全息光束成形技术成形为期望的模式。

在这种情况下，圆曲线被选为主要研究对象。这里，x₀(t)=R_icost，y₀(t)=R_isint，N=100，R₁=1.6 mm，R₂=1.9 mm，m₁=4，m₂=-4且N=|m₁− m₂|，其中，R_i是控制光束半径的参数，N是圆形厚度，m₁和m₂是两个叠加光学涡旋光束的拓扑荷，N是环上光学涡旋的数量。图2(b1)显示了光学涡旋晶格的相位项。假设l=3，重塑相位ψ₀和最终截断相位分别如图2(b2)和(b3)所示。

 

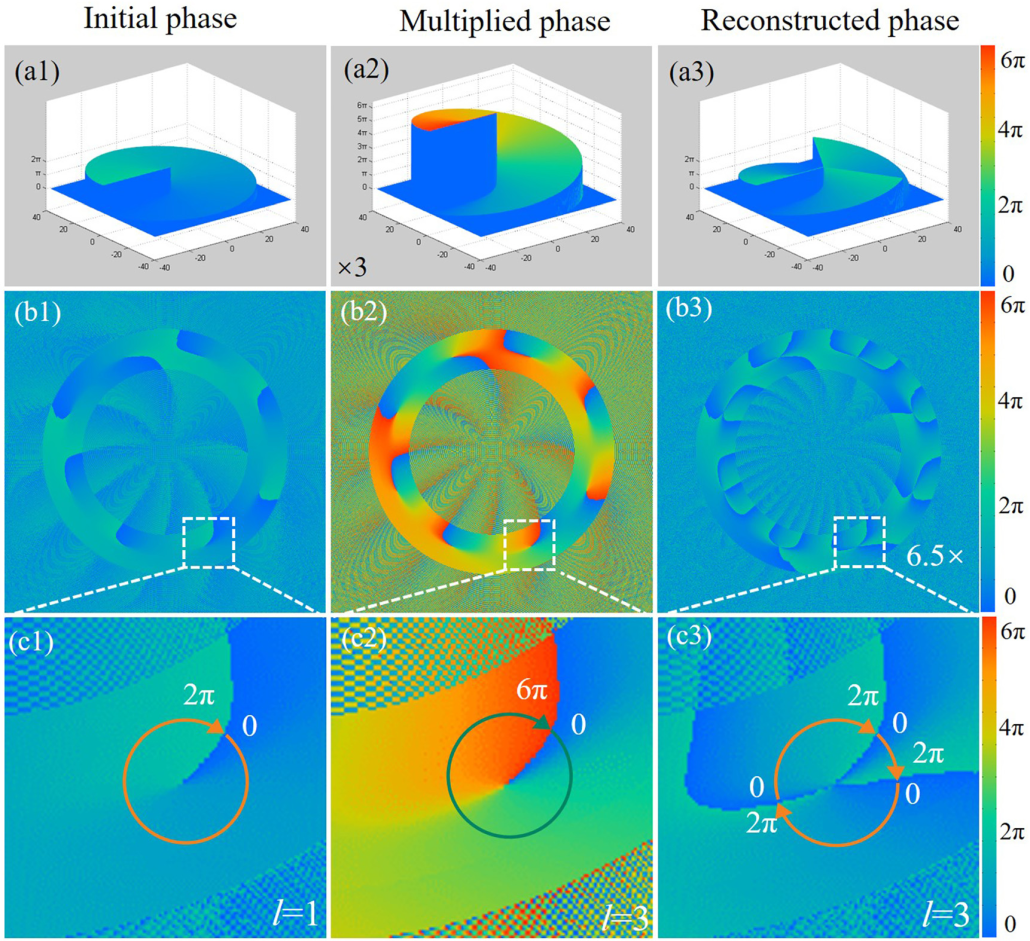
图2 通过相位乘法生成高阶拓扑荷。（a1）–（a3）分别为光学涡旋的初始相位、倍增相位和高阶相位。（b1）–（b3）光学涡旋晶格的相位重建。（c1）–（c3）特定光学涡旋相位的放大模式。

为了生成和验证所提出方法的有效性，研究人员进行了实验，如图3所示。532 nm激光束在扩展和准直后照射空间光调制器。光束由空间光调制器调制并反射到4F系统上，该系统由两个透镜（L1和L2）组成，具有相同的焦距（15 cm）。最后，它被电荷耦合器件记录在第二傅里叶平面上。虚线包围的光路是执行干涉的参考光路。

 

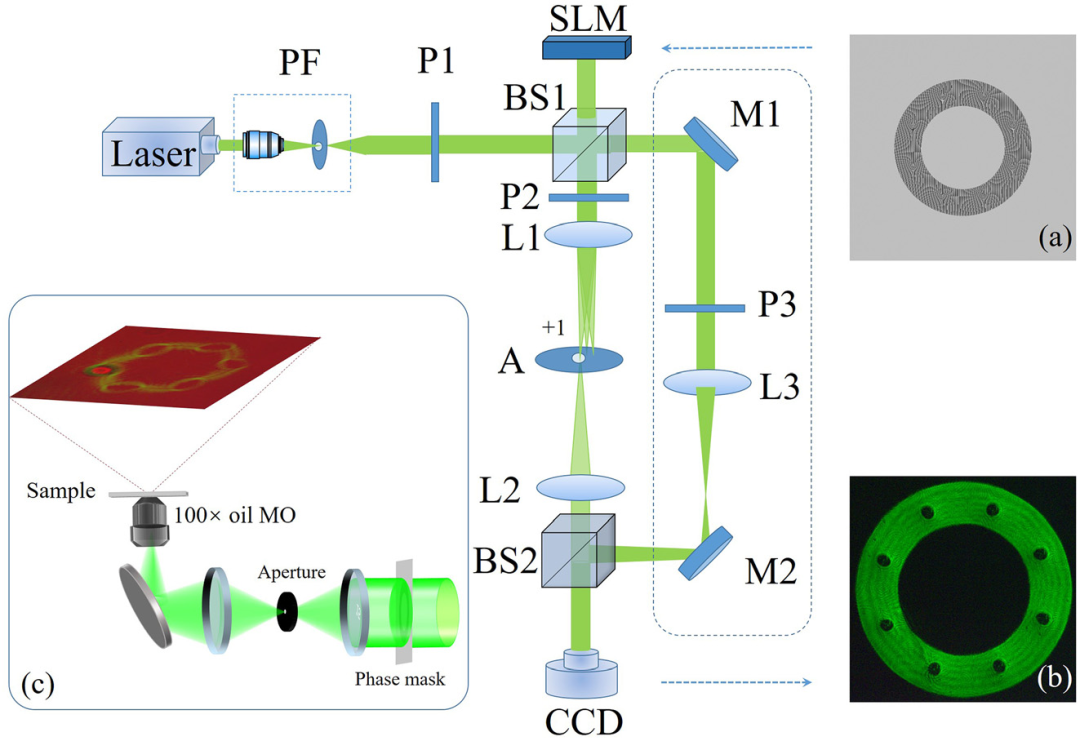
图3 实验装置示意图。PF，针孔滤波器；P1–P3，偏振器；BS1和BS2，分束器；SLM，空间光调制器；L1–L3，凸透镜；A，孔径；M1和M2是反射镜；CCD，电荷耦合器件。（a）调幅相位掩模，（b）CCD记录的高阶光学涡旋晶格的强度以及（c）粒子操纵模块。

实验中，研究人员设计了一个二进制掩模来消除杂散光，如图3(a)所示。它表示为T=bw[A（r，θ）]×exp{i[1φ（r，θ）+2πx/d]}，其中，bw是一个二元函数，d是闪耀光栅的周期。由于光学涡旋晶格是在空间光调制器平面上产生的，因此，4F系统被用于在所需位置输出和记录高阶光学涡旋晶格。

为了验证光学涡旋的存在并确定它们在高阶光学涡旋晶格中对应的拓扑荷，研究人员使用球形光束作为参考光来执行干涉。图4说明了强度模式和干涉图。暗核的尺寸随着l的增加而增加。在每个暗核的相应位置处的干涉图图案中出现了螺旋叉条纹图案。结果表明，高阶光学涡旋晶格中存在光学涡旋。此外，光学涡旋的拓扑荷由叉数减1确定，这与默认值l一致。因此，在这种情况下，成功生成了高阶光学涡旋晶格（图5）。

 

图4 高阶光学涡旋晶格和球面波的干涉图。（a1）–（a3）分别为l=1、2和3的实验强度模式以及（b1）–（b3）其相应的干涉图。

 

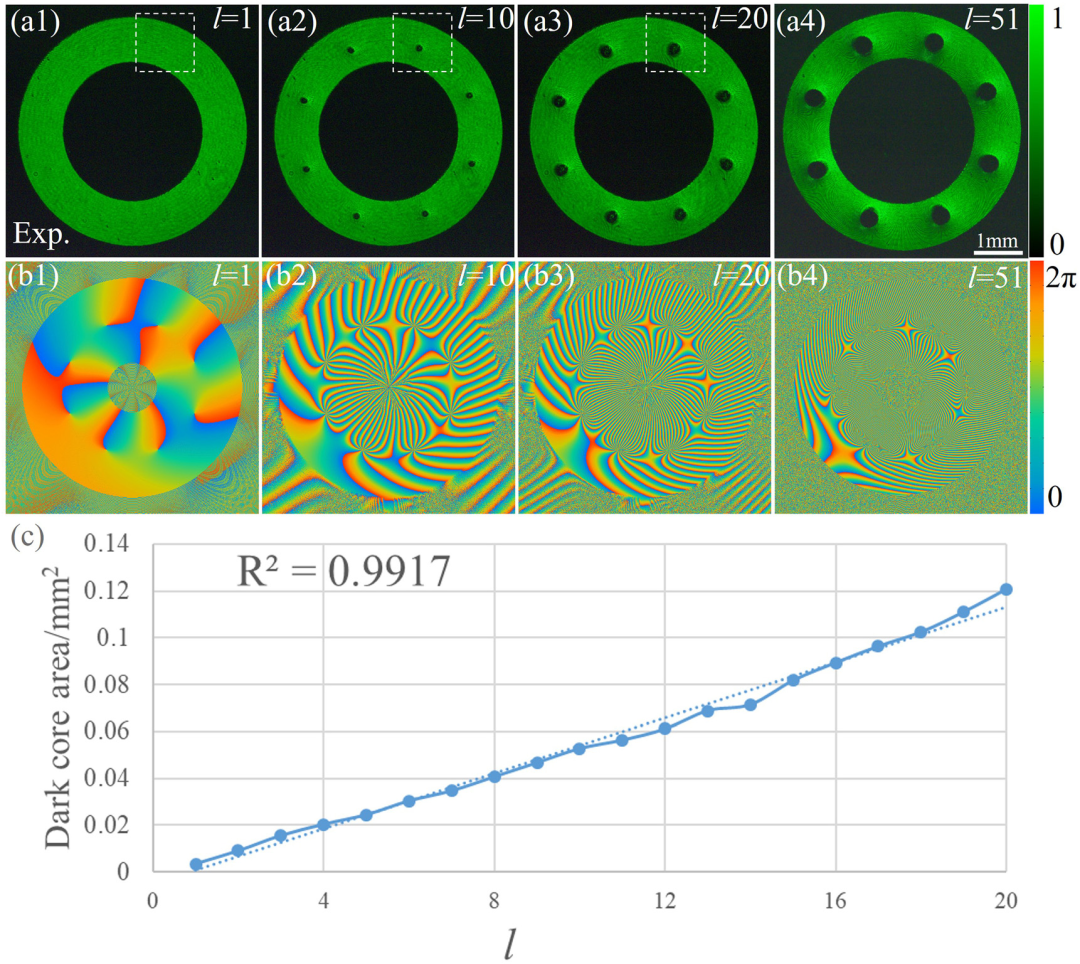
图5（a1）–（a4）具有不同拓扑荷（分别为1、10、20和51）的高阶光学涡旋晶格强度模式。（b1）–（b4）顶行的对应相位图案。（c） 暗芯面积与拓扑荷。

为了赋予轨道角动量在高阶光学涡旋晶格中的重要作用，它被用作具有lħ轨道角动量的每个光子的l的关键参数。晶格中光学涡旋的轨道角动量容量由最大值l决定。在这里，倍增次数最多为51次（即，l=51）。此外，暗核的结构逐渐改变为超过该值的水滴形状（l＝51）。然而，如果分别仔细设计和布置相位掩模和实验元件，则可以获得具有增加的轨道角动量的高阶光学涡旋晶格用于特殊应用。

为了利用高阶光学涡旋晶格中的轨道角动量，必须演示和分析轨道角动量和能量流的分布。接下来，研究人员改变了高阶光学涡旋晶格的参数以加厚足够光子的强度环，其中，n＝150，l＝1、10和20。在实验中，在解中很难确定轨道角动量。因此，轨道角动量和能流通过先前方法进行了数值计算。

利用上述理论，研究人员对高阶光学涡旋晶格的能流和轨道角动量进行了数值模拟。为了进行比较，暗核的大小被设计为随着l的增加而恒定。图6(a1)–(a3)显示了包含能流的强度模式。其中，白色箭头表示流动的方向和大小。为了观察细节，放大了特定的光学涡旋，如图6(b1)–(b3)所示。可以看到，在每个光学涡旋周围形成了能流的环电流。此外，环电流随着l的增加而急剧增加。这一趋势也出现在轨道角动量的密度模式中[图6(c1)–(c3)]，这是利用特定光学涡旋的中心作为轨道角动量旋转轴来计算的。

 

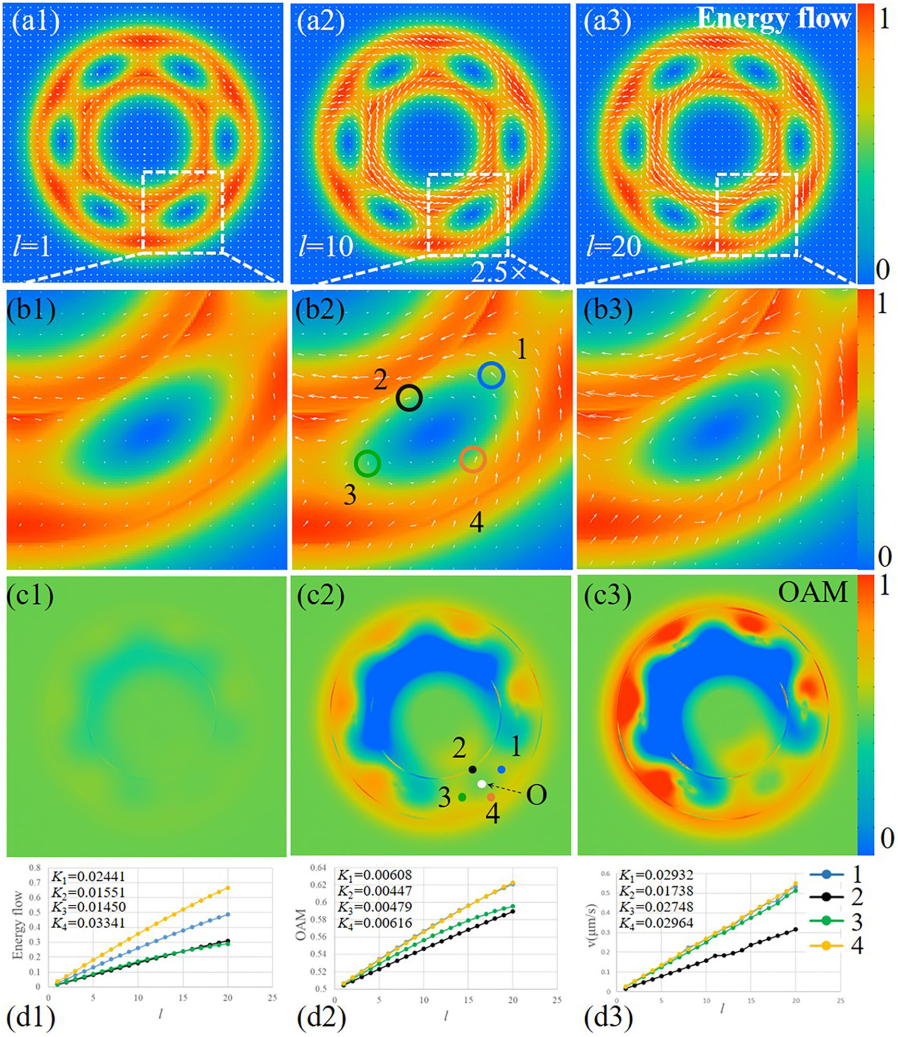
图6 能量流和轨道角动量随l的增加而变化。（a1）–（a3）能流，（b1）–（b3）晶格中光学涡旋的局部放大以及（c1）–（c3）轨道角动量密度分布。对称轴位于特定光学涡旋的中心，即O点（d1）、（d2）和（d3）。能流、轨道角动量和旋转速度分别在特定点与拓扑荷的关系。注意，能流和轨道角动量分别被归一化。

为了定量分析能量流、轨道角动量和转速随l增加的变化，研究人员计算并绘制了第二行标记的四个采样点的数据[图6(d1)、(d2)和(d3)]。其中，在实验条件下，通过文献中的方法对旋转速度进行了数值模拟。结果表明，能流、轨道角动量和旋转速度随l的增加而单调增加。此外，能流的放大倍数、轨道角动能和旋转速度近似等于l的值。例如，与l＝1相比，当l＝10和20时，能流和轨道角动量的时间分别等于9.7和17.8。对于特定采样点，拟合线的斜率不同，而由于初始值不同，时间大致相等。结果表明，高阶光学涡旋晶格中的单位光学涡旋可以用于旋转和自旋不同尺寸的微粒。

为利用光学涡旋晶格中的轨道角动量，即赋予其重要作用，研究人员进行了微粒操纵实验。选择酵母细胞作为样品，以突出其在生物科学中的应用。使用油浸显微镜物镜将高阶光学涡旋晶格[图3(c)]聚焦到样品上。

实验中，研究人员进行了三组实验来验证轨道角动量的能力。首先，用l＝1的高阶光学涡旋晶格照射5-8 μm的酵母细胞20s。细胞被困在光学涡旋中，具有轻微的布朗运动。随后，光束被转换成l＝6的高阶光学涡旋晶格，细胞在轨道角动量的影响下开始旋转。该过程，如图7(a1)-(a5)所示。在实验中，酵母细胞以一定角度旋转后停止旋转（∼90°）。在细胞旋转过程中，它们总是达到平衡，其中，轨道角动量不能提供足够的扳手力来继续旋转。这种现象主要是由暗核和酵母细胞之间的形状匹配造成的。如果占据光学涡旋的暗核是一个完美的圆，细胞就会不停地旋转。粒子的取向位置可以通过形成暗核的结构来确定。因此，晶格中光学涡旋的轨道角动量将在细胞旋转中起主导作用。

 

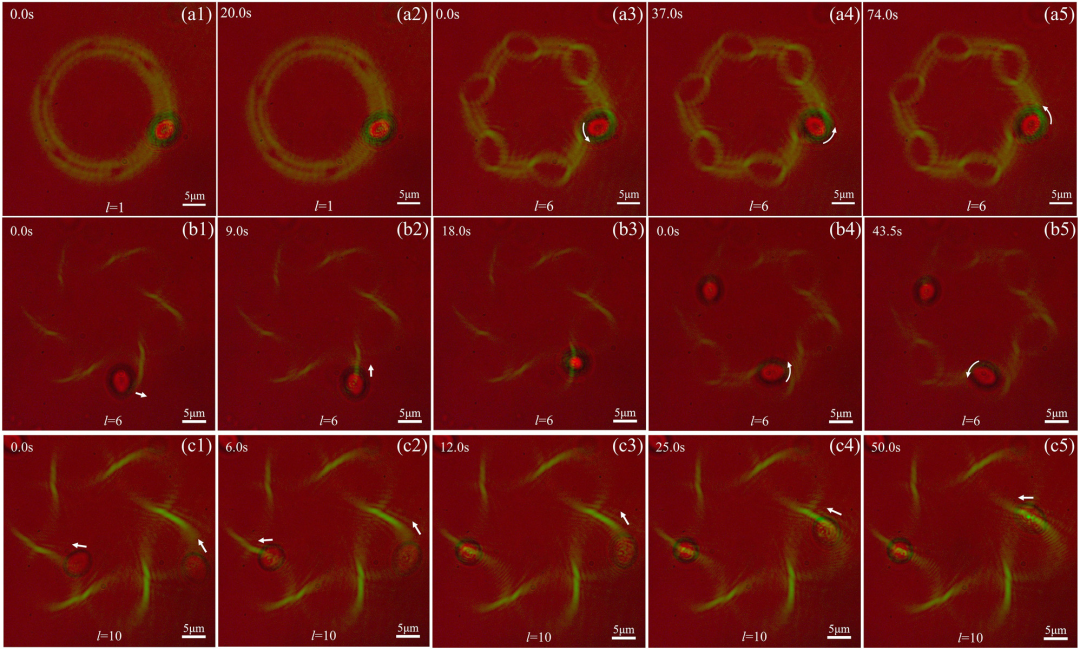
图7 通过高阶光学涡旋晶格操纵酵母细胞。（a1）–（a5）通过l=1的高阶光学涡旋晶格照射酵母细胞，随后将其转换为l=6。

此外，轨道角动量可以实现复杂的运动，包括围绕光学涡旋的旋转（第二行展示了这些特性）。用l＝10的高阶光学涡旋晶格交替地照射酵母细胞。这里，光学涡旋的半径大于酵母的半径，从而有利于光学涡旋周围的环进行捕获，然后，在施加轨道角动量时旋转。接下来，l被更改为6，酵母的旋转恢复，如图7(b1)–(b5)所示。与单个光学涡旋光束相比，光学涡旋晶格的优点之一是它包含多个光学涡旋。因此，高阶光学涡旋晶格可以同时操纵多个粒子。如图7(c1)-(c5)所示，通过同时旋转两个酵母细胞来证明和验证了这种能力。根据需要，可以使用更复杂的拓扑荷的组合来获得细胞的更复杂的运动。

到目前为止，轨道角动量在高阶光学涡旋晶格中显示出巨大的能力。为了满足多粒子操纵的特殊要求，高阶光学涡旋晶格的多功能模式应该被自由控制。由于任意曲线技术，生成了具有特定模式的高阶光学涡旋晶格，例如，三角形、心形和六边形模式，如图8所示。晶格中每个光学涡旋的拓扑电荷乘以10。尽管采用了相同的模式，但曲线函数不是唯一的。由于曲线函数的差异，研究人员根据实验调整了不同的曲线参数。图8显示了三种模式的强度和相应的相位分布。对于三角形高阶光学涡旋晶格，方程和参数设置为x₀(t)=R_i(-2cost+0.54cos2t)，y₀(t)=R_i(-2cost−0.54cos2t)，n=100，R₁=0.8 mm，R₂=1.1 mm，m₁=3，m₂=-3。对于心形高阶光学涡旋晶格，方程和参数设置为x₀(t)=|R_i(3cost−2cos2t)|，y0(t)=-Ri(2cost−3cost), n=100，R₁=0.8 mm，R₂=0.9 mm，m₁=3，m₂=-3。对于六边形高阶光学涡旋晶格，方程和参数设置为x₀(t)=R_icost(1−0.035cos6t)，y₀(t)=R_icost(1−0.035cos6t)，n=100，R₁=1.6 mm，R₂=1.9 mm，m₁=3，m₂=-3。使用任意曲线函数，可以根据需要确切地产生相应的高阶光学涡旋晶格。

 

图8 具有多种模式的高阶光学涡旋晶格。（a1）–（c1）三角形、心形和六边形高阶光学涡旋晶格的强度模式。（a2）–（c2）（a1）–（c1）的对应相位分布。在所有情况下，l=10。

与全息光镊相比，基于高阶光学涡旋晶格的光镊可以捕获多个粒子，同时执行复杂的运动，特别是自旋和轨道旋转。所提出的高阶光学涡旋晶格的暗核和轨道角动量是关键，这将促进新的潜在应用，而这些应用仅限于想象。从实验来看，由于暗核的不对称，酵母细胞没有旋转一个完整的周期。通过精确修改单位光学涡旋的大小、结构和强度分布，可以实现具有完整周期的旋转，甚至整个光学涡旋晶格上的轨道旋转。这个问题将在不久的将来进行研究。此外，力场分布和多个粒子，特别是纳米颗粒的更复杂的运动，是应该很快进行广泛研究的其他领域。

总之，研究人员提出了采用相位倍增和任意弯曲技术的具有可控模式的高阶光学涡旋晶格。为了保证光束质量，晶格中每个光学涡旋的轨道角动量阶数增加到51，超过了传统光学涡旋晶格的极限。因此，利用并释放了高阶光学涡旋晶格中每个光学涡旋的轨道角动量。酵母细胞的操纵表明，高阶光学涡旋晶格可以在轨道角动量的影响下诱导颗粒的复杂运动。结果可以为未来捕获和操纵多种微粒铺平道路，特别是在生物科学中。