单频光纤法布里-珀罗布里渊激光器

受激布里渊散射激光器具有超窄的线宽，在通信和计量领域具有广泛的应用前景。基于各种类型谐振腔的受激布里渊散射激光器已经被实现，包括光纤环形谐振腔、硅基二氧化硅材料圆盘谐振腔和氟化钙微谐振腔。其中，全光纤谐振器可以很容易地引入到光纤系统中，而不需要复杂的光纤谐振耦合机制。最近，光纤受激布里渊散射激光器作为稳定的窄线宽光源已经在光学原子钟中实现。

典型的谐振器具有恒定的自由光谱范围，且纵模间隔相等。因此，一阶Stokes模式的受激布里渊散射激光可以作为二阶Stokes模式的泵浦光，发生级联激射。尽管受激布里渊散射激光器的级联激射在一些应用中得到了应用，例如微波源，但是对于需要单频激光器的应用，它限制了输出功率。通过改变泵浦光与谐振腔的耦合速率，研究人员在圆盘谐振腔中实现了对级联激射的抑制。然而，这种方法并不直接适用于光纤谐振器。在光纤中实现单频受激布里渊散射激射的另一种方法是利用长光纤布拉格光栅中的分布反馈，在光纤布拉格光栅的中心产生π相移。采用高非线性光纤中12.4 cm长的分布反馈光纤布拉格光栅和标准单模光纤中50 cm长的分布式反馈光纤布拉格光栅，研究人员实现了阈值为30 mW和128 mW的单频受激布里渊散射分布反馈激光输出。在这些工作中，采用了单程泵浦。为了在短谐振腔长度的标准单模光纤中实现低阈值、单频受激布里渊散射激光，共振泵浦是有用的。

首先，制作光纤法布里-珀罗谐振腔的曝光装置，如图1(a)所示，特别是一种精确的谐振腔长度控制方法，以使谐振腔自由光谱范围与布里渊频移相匹配。为了制作高Q值法布里-珀罗谐振腔，通过扫描相位掩模板上的深紫外激光光斑，在无载氢的标准Ge掺杂单模石英光纤（SM800, Fibercore）的纤芯上连续刻写两个光纤布拉格光栅反射镜。剥离后的光纤附着在石英玻璃制成的相位掩模板上。相位掩模板长度为50 mm，覆盖了光纤谐振腔的整个长度。研究人员使用了波长为213 nm的调Q深紫外激光器，平均输出功率和脉冲重复频率分别约为100 mW和15 kHz。沿光纤方向的光斑直径约为6 mm，光斑的位置由计算机控制的电动平台上的反射镜控制。此外，深紫外光束线中计算机控制的机械快门控制了曝光时间。虽然电动平台可以以亚毫米级的精度控制光纤上反射镜之间的距离，但由于布里渊增益带宽较窄，约为30 MHz，而在852 nm波长处的布里渊频移约为19.7 GHz，因此，需要对自由光谱范围进行更高精度的优化。为了使布里渊频移与谐振腔的自由光谱范围在几兆赫兹内匹配，研究人员利用电动平台粗调第二个光纤布拉格光栅反射镜的位置，并利用第二个光纤布拉格光栅反射镜的曝光时间来控制自由光谱范围，同时用频率可调的外腔半导体激光器监测自由光谱范围。由于进入光纤布拉格光栅反射镜的穿透长度随着曝光时间的变化而变化，因此，可以通过控制曝光时间来精确控制谐振腔长度。根据观测到的自由光谱范围计算得到谐振器的有效长度约为5 mm。每个光纤布拉格光栅的长度约为10 mm，光纤上暴露区域的边长约为20 mm。每个光纤布拉格光栅曝光时间约为6 min。图1(b)和(c)分别为光纤布拉格光栅反射镜和制作的光纤谐振腔的典型透射光谱。利用外差技术探测传输信号，其中从与探针相同的源获得的频移激光作为本振（图1(a)），测量实现了约50 dB的高信噪比。值得注意的是，由于制备的光纤布拉格光栅反射镜具有较大的色散，谐振器的谐振峰在透射谱中的间隔并不均匀，如图1(c)所示。这些共振峰的特征结构具有重要作用。

 

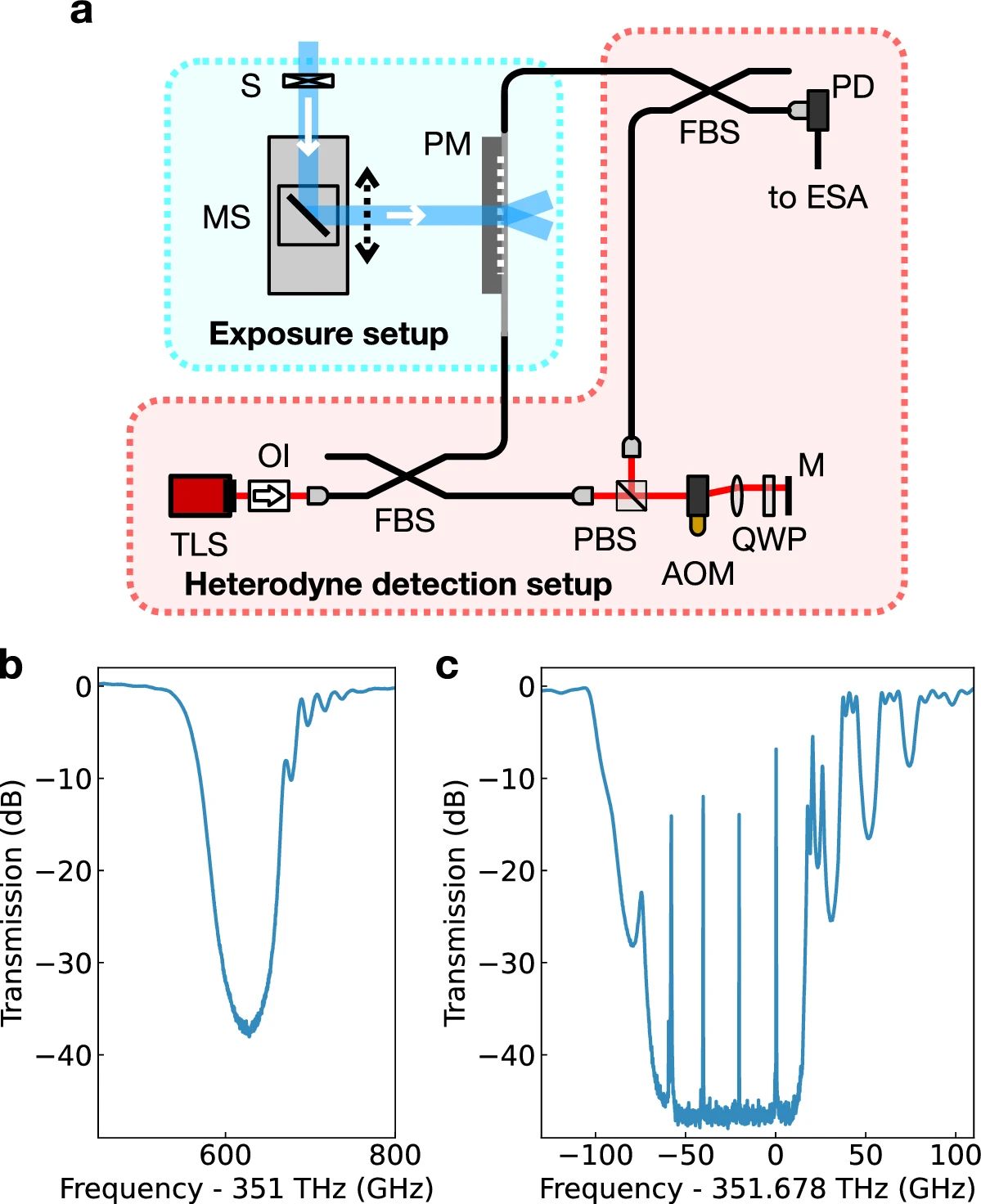
图1 （a）光纤谐振器制作装置。使用计算机控制的载物台在相位掩模板上扫描一束深紫外光束（蓝色粗线）。利用外差装置测量谐振腔的透射谱。本振光场具有双程配置下使用声光调制器产生的频率偏移。S：机械快门；MS：机动阶段；PM：相位掩模；TLS：可调谐激光光源；OI：光隔离器；FBS：光纤分束器；AOM：声光调制器；QWP：四分之一波片；M：镜子；PD：光电探测器；ESA：电子频谱分析仪。(b) 制作的光纤布拉格光栅透射谱。光栅强度约为490 m^-1。(c) 制备的光纤法布里-珀罗谐振腔的透射谱。频谱中心处平坦信号的电平对应频谱分析仪的电噪声基底。

谐振腔输出的布里渊位移场的光谱分量随泵浦功率的变化关系，如图2(d)所示，显示了清晰的阈值行为。利用外差技术探测输出，其中电光调制器产生的泵浦场的边带分量用作本振（图2(c)）。

 

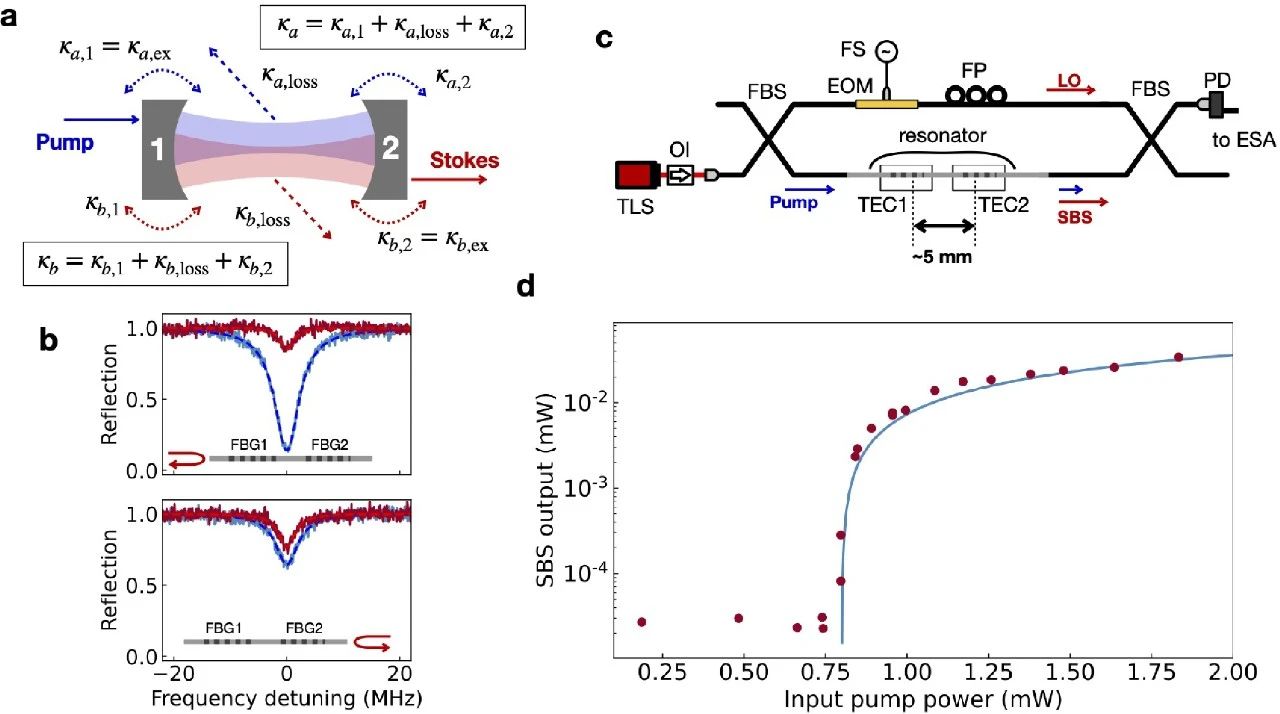
图2 (a) 泵浦和Stokes模式的谐振腔场衰减率的关系。(b) 谐振腔谐振对泵浦光场和第一Stokes光场的反射谱。上：以光纤布拉格光栅1为输入耦合器的反射光谱；下：以光纤布拉格光栅2作为输入耦合器的反射光谱。实线对应于（蓝色）泵浦光场和（红色）第一Stokes光场的共振，虚线表示Lorenzian拟合数据。(c) 测量装置。谐振腔长度约为5 mm。TEC1和TEC2分别为稳定光纤布拉格光栅1和光纤布拉格光栅2反射率的温控单元。电光调制器处的调制频率为19.6 GHz。FS：频率合成器。(d) 受激布里渊散射输出的阈值行为。圆圈表示实验观测值，实线表示计算结果。

为了分析受激布里渊散射输出随泵浦功率的变化，研究人员使用泵浦和Stokes模式的耦合模方程，一阶Stokes模的输出功率是泵浦功率的函数。这里考虑一阶Stokes模；泵浦和Stokes模式的外部耦合率[图2(a)]；利用反射光谱进行了实验评估，如图2(b)所示。除了这些评估值，利用观察到的阈值泵浦功率（0.8 mW），可以计算出第一个Stokes模式的谐振腔输出功率随泵浦功率的变化。计算结果与观测结果符合较好，如图2(d)所示。

接下来，研究人员搭建了一对受激布里渊散射激光装置来获得两个独立的受激布里渊散射激光源之间的拍频信号。实验装置，如图3(a)所示。两个谐振器在不同频率下对泵浦产生谐振，谐振器自由光谱范围略有不同，相差17 MHz。因此，拍频信号有两个频率成分：与泵浦光频率差对应的频率成分和由自由光谱范围差值进一步偏移的频率成分。拍频信号随泵浦激光频率的变化，如图3(b)所示。将频率的原点设为泵浦光之间拍频信号的中心。由于光纤布拉格光栅处的双折射，谐振器对两个正交偏振具有不同的谐振频率和自由光谱范围。因此，当每个泵浦光偏振优化为谐振腔共振时，可以观察到受激布里渊散射激光器之间的拍频信号，该拍频信号对第一个Stokes光场有另外一个共振。如图3(b)所示，可以比较使用不同泵浦偏振的受激布里渊散射激光器前后的拍频信号。最后，给出了受激布里渊散射激光器之间拍频信号的详细视图，如图3(b)插图所示。目前，受激布里渊散射激光器之间拍频信号的观测线宽约等于泵浦激光器之间的线宽且受到电频谱分析仪分辨率带宽的限制。受激布里渊散射激光器的线宽取决于泵浦光的相位噪声，但受到谐振腔和声子阻尼的强烈抑制。对于谐振腔参数，线宽缩减比约为100。对法布里-珀罗谐振腔受激布里渊散射激光器进行更详细的线宽和稳定性测量是未来工作的一个课题。

 

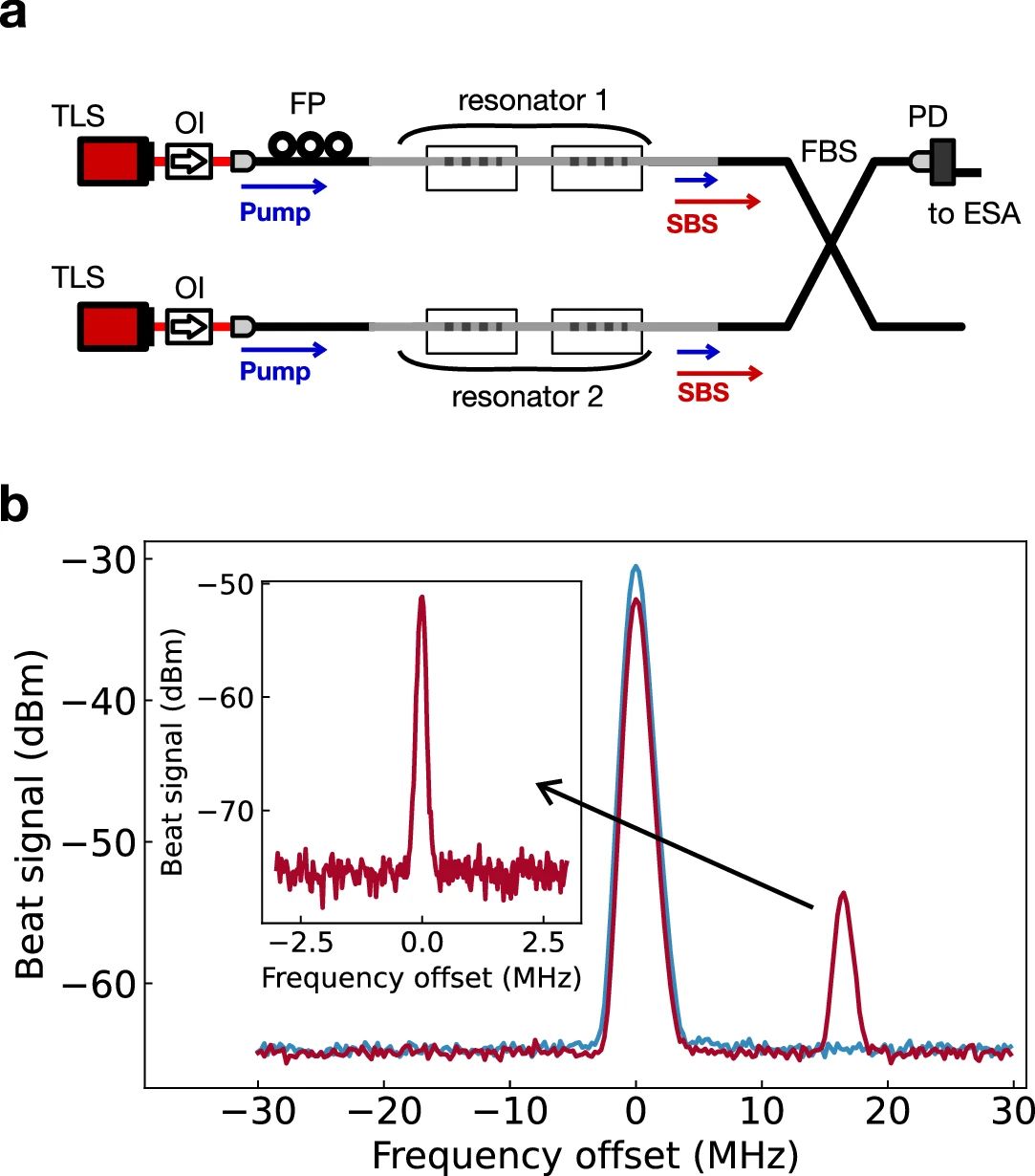
图3 (a) 拍测量。(b) 两个独立的受激布里渊散射激光器之间的拍频信号。蓝色实线是通过调节其中一个泵浦光的偏振实现受激布里渊散射激光，红色实线是通过调节两个泵浦光的偏振实现受激布里渊散射激光。两种结果均为20次测量的平均值。插图显示了独立受激布里渊散射激光器之间拍频信号的详细视图。频率原点设置为拍频信号的中心。主图和插图的分辨率带宽分别为1 MHz和100 kHz。

典型的谐振器在很宽的频率范围内具有恒定的自由光谱范围，且纵模间隔相等。利用这样的谐振腔，输入泵浦光产生的一阶Stokes光场可以作为二阶Stokes光场的泵浦光场。通过这种级联的布里渊散射，多模受激布里渊散射激射一般在各种谐振腔平台中观察到，例如光纤法布里-珀罗谐振腔、光纤环形谐振腔和圆盘谐振腔。相比之下，与光学谐振腔中使用的标准多层介质反射镜相比，光纤布拉格光栅反射镜具有更大的色散。如图1(c)所示，谐振器具有多个谐振峰，但它们具有不同的频率间隔（泵浦模与第一Stokes模之间的频率为19.70 GHz，第一Stokes模与第二Stokes模之间的频率为19.53 GHz）。

因此，由于谐振腔布里渊增益可以忽略不计，级联布里渊散射和高模式受激布里渊散射激光的强抑制是可望的。为了证实受激布里渊散射激光器的这一特性，研究人员测量了具有较高泵浦功率的谐振腔输出场中的第一Stokes分量，如图4所示。在该测量中，通过改变反射镜温度优化了光纤布拉格光栅反射镜反射率，实现了更低的一阶受激布里渊散射激射泵浦功率阈值。

 

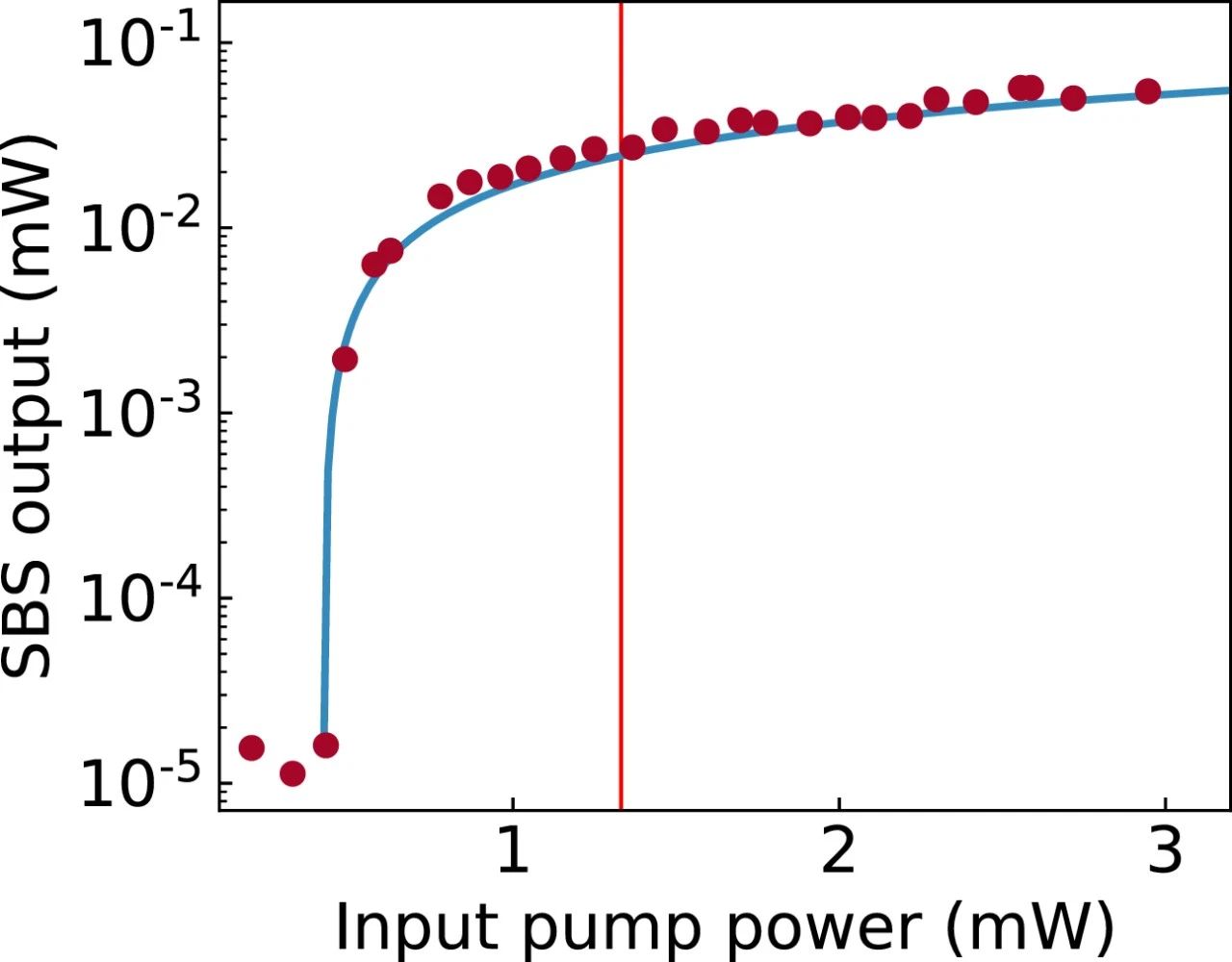
图4 光纤法布里-珀罗谐振腔中级联受激布里渊散射激射的抑制。圆圈为谐振腔输出的第一Stokes分量随输入泵浦功率变化的实验观察。实心曲线是只包含一阶Stokes模式的计算结果。垂直实线表示二阶Stokes模的受激布里渊散射激光的阈值泵浦功率。谐振器参数测量，如图2所示。

为了与谐振腔对二阶Stokes模有谐振模式的情况进行对比，研究人员计算了二阶受激布里渊散射模开始振荡（图4中竖直实线）的阈值泵浦功率。这里，假设第一和第二Stokes模具有相同的场衰减率和布里渊增益。若二阶Stokes模存在谐振模式，则一阶Stokes模的输出功率应在二阶受激布里渊散射激光的阈值泵浦功率处下降。然而，如图4所示，一阶Stokes模的输出功率并没有显示出级联激射的开始，仅使用一阶Stokes模（图4中曲线实线），模型对观测到的输出功率给出了合理的解释。这一结果表明光纤法布里-珀罗谐振腔能够在高泵浦功率的单模受激布里渊散射激光器中工作。此外，研究人员使用独立的可调谐激光源作为本振源，对外差测量了第二Stokes模式对应的光谱成分，并证实了在高达3 mW的泵浦功率下没有该成分。在泵浦功率约为3 mW的情况下，测量被限制在比第一Stokes模信号低30 dB的噪声底。

综上所述，研究人员发展了一种适用于单频受激布里渊散射激光器应用的高Q值光纤法布里-珀罗谐振腔的制备方法。谐振腔长度最短，使得自由光谱范围在852 nm泵浦激光下匹配到19.7 GHz的布里渊频移。通过相位掩模法将谐振腔直接制作成标准单模光纤，全光纤受激布里渊散射激光器比典型的光纤环形谐振腔要小得多。此外，制作的光纤布拉格光栅中的强色散会引起不同自由光谱范围的谐振器共振。因此，级联激射被强烈抑制且没有观察到二阶Stokes模式的激射，其泵浦功率比一阶Stokes模式的阈值泵浦功率强7倍，这受限于所使用的实验装置。这项研究实现了紧凑、稳定、高效的窄线宽光源。