穿越时空的湍流之旅
唐太宗曾有言:“以史为镜,可以知兴替”。为了从历史的角度理解湍流的发展,今天,我们就走近湍流,来一场穿越时空的旅行。
在流体力学方面,达·芬奇总结出河水的流速同河道宽度成反比,这也是连续性方程最早的描述。他还通过对鸟翼运动的研究,于1493年首次设计出一个飞行器。当然,达芬奇在流体力学领域最大的贡献仍然是他基于对流体的观察和思考所绘制的图画。

作为经典力学的开创者,牛顿大帝当然也没有放过流体力学。经过大量的实验研究,牛顿于1686年提出了著名的“牛顿内摩擦定律”——流体的内摩擦力(即粘性力)的大小与流体的性质(粘性系数μ)有关,并与流体的速度梯度和接触面积成正比。
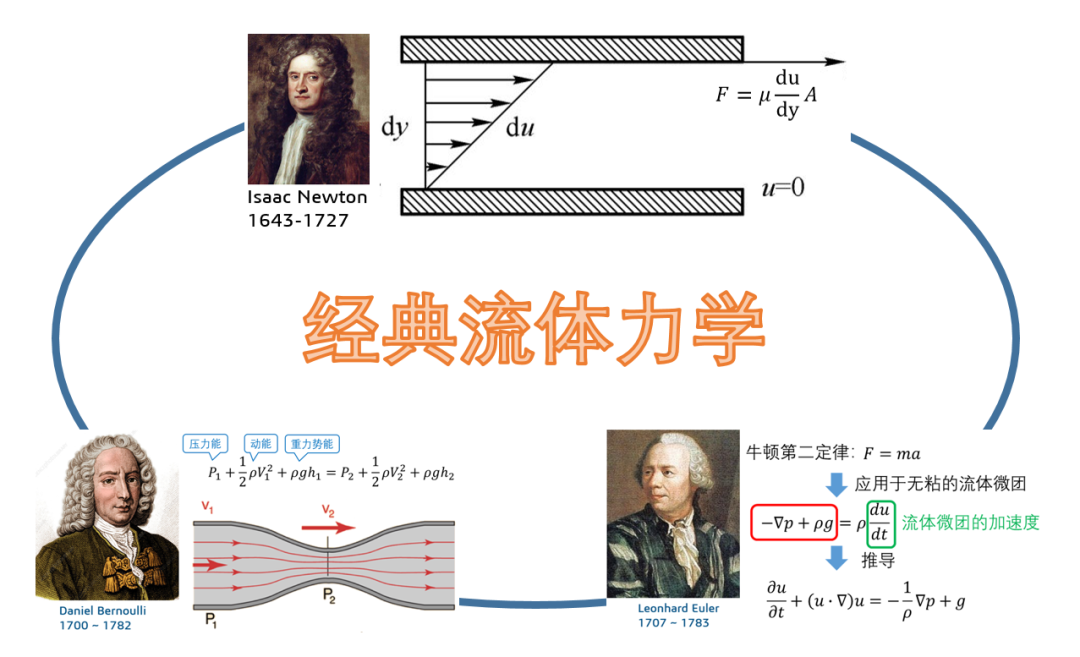
1738年,丹尼尔·伯努利在经典著作《流体动力学》中提出了著名的伯努利原理:流体速度的增加与静压的降低或流体势能的降低同时发生, 14年以后,丹尼尔一生的挚友——欧拉才给出通用形式的伯努利方程。当然,欧拉大神对于经典流体力学更大的贡献则是将微分方程应用到了流体力学的领域,并提出了影响后世的欧拉方程,即牛顿第二定律施加到理想流体上的微分方程。
直到1822年,纳维公开发表了关于流体运动的文章,从分子运动层面阐述了相对运动产生的分子间作用力,文章提到:从大量的经验来看,压力并没有明显地影响运动流体各部分之间的分子作用所产生的阻力,而这些阻力来源于相邻分子的速度大小或方向的差异,即分子间的相对速度。另外,纳维在文章中还明确提及了流动的“非线性”,用数学层面的语言解释了某种混乱的流动。

可是让流体江湖万分敬仰的N-S方程却不是一个省油的灯,正如我们在之前的文章中调侃过的,N-S方程就仿佛流体江湖的“葵花宝典”,所有人都知道修炼成功之后便可纵横武林,但是欲练此功就必须要“挥刀自宫”。对于N-S方程来说,这最痛的一刀便是方程中的对流项u·▽u,它具有二阶非线性,如同一座大山一样挡在求解者的面前。而非线性本身便是湍流的一大特征。从此N-S方程便和湍流开启了长达一百多年的纠缠,直至今日。
法国著名的机械工程师和数学家Saint-Venant首先在公开发表的文章中区分了 “常规”和“动荡”两种流动状态。后来,人们对这两种流态之间的过渡产生了浓厚的兴趣,大家开始寻求一种解释这种过渡的机制,并寻求一种表征流动不规则、不稳定或者扭曲的标准。



或许是汤姆森在流体力学领域的地位还不够显赫,他提出“湍流(turbulence)”很长一段时间以后并未得到整个学界的广泛认可。直到20世纪初,Boussinesq开始在论文中统一使用湍流(turbulence)一词。随后,现代流体力学的祖师爷普朗特和他的徒子徒孙们也开始全面使用湍流(turbulence)一词。再之后,湍流不仅仅成为一个所有人认可的名词,更是成为了一个专门的研究领域。
不过所幸,对于很多工程问题,我们并不需要完全求解湍流。比如工程上更关心流动的压力损失和平均速度分布,而非湍流的细节。雷诺实验五年以后,雷诺才幡然醒悟,既然流动未可知,不妨使用统计学的思想——对N-S方程进行平均,把瞬时速度u分解为时均速度ū和脉动速度u’,代入N-S方程即可得到雷诺平均的N-S方程,也就是RANS。
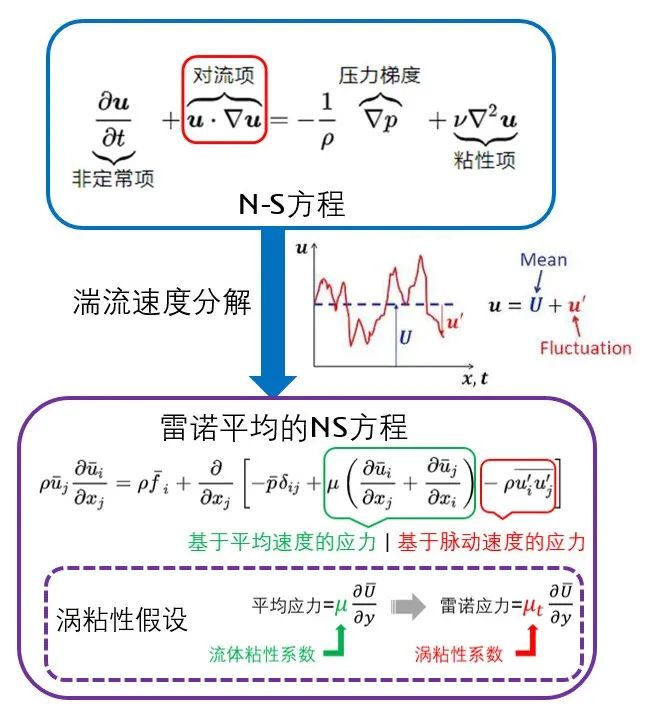
我们知道流体的粘性来自于分子自由运动产生的掺混,与分子运动自由程密切相关;而对于涡粘性,也可以类似的定义湍流脉动掺混的长度,称之为混合长度,其物理意义为流体微团耗散前所经历的距离,因此脉动速度可以表示为混合长度与Y向速度梯度的乘积,而涡粘性系数则可以相应的表述出来。因此,只要知道了混合长度,便可以明确涡粘性系数,进而求解雷诺平均的N-S方程。
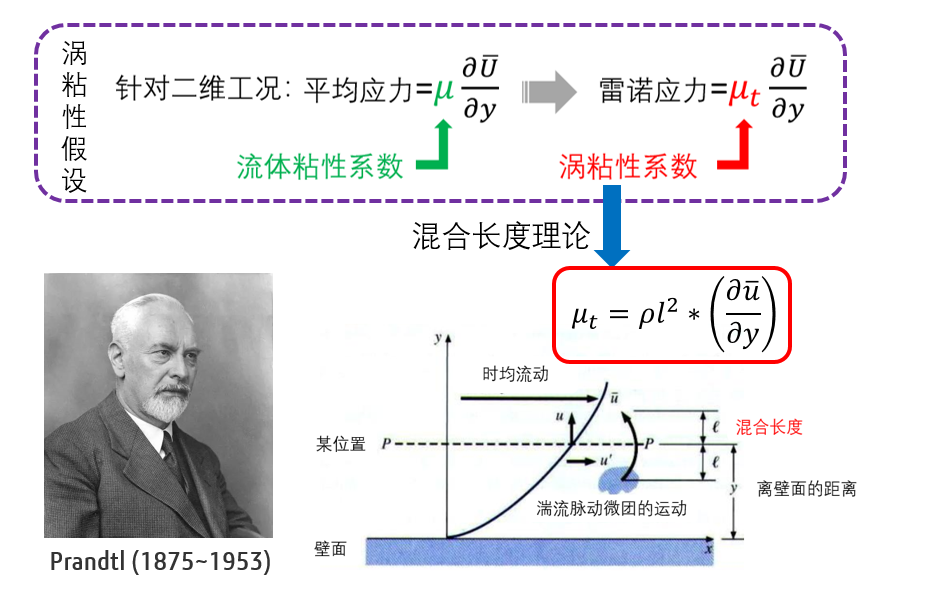
混合长度模型是代数模型,相当于直接用代数公式定义了涡粘性系数,被称为零方程模型。而我们熟知的k-epsilon模型及其变种(如k-omega模型等),也属于涡粘性模型,该模型针对混合长度继续演化,将其表示为湍动能k、湍流耗散率epsilon和湍流脉动速度的函数,而涡粘性系数便可由k和epsilon导出。普朗特之后,湍流的求解再次进入到了一个全新的时代,直至今日。
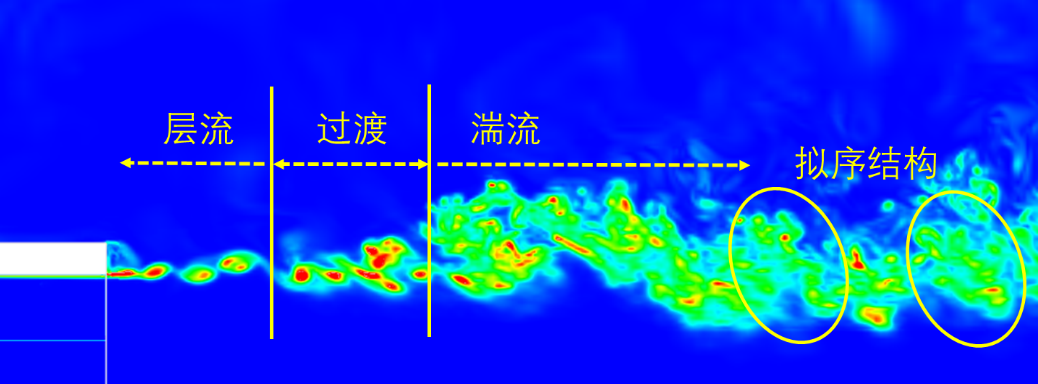
下图为某风洞喷口的剪切层涡量分布,在剪切层最开始发展的阶段,流动呈现明显的规律性,涡的大小和强度都比较单一,在涡的内部仍可以认为是层流的状态。而随着流体向下游发展,掺混作用增强,大涡不断破碎为小涡,小涡则进一步破碎并逐渐消耗,化为流体的内能,这个阶段才能称之为完全发展的湍流。

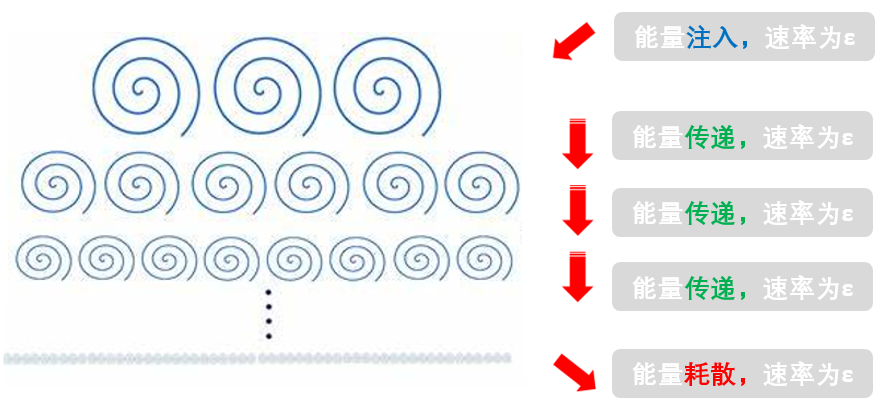
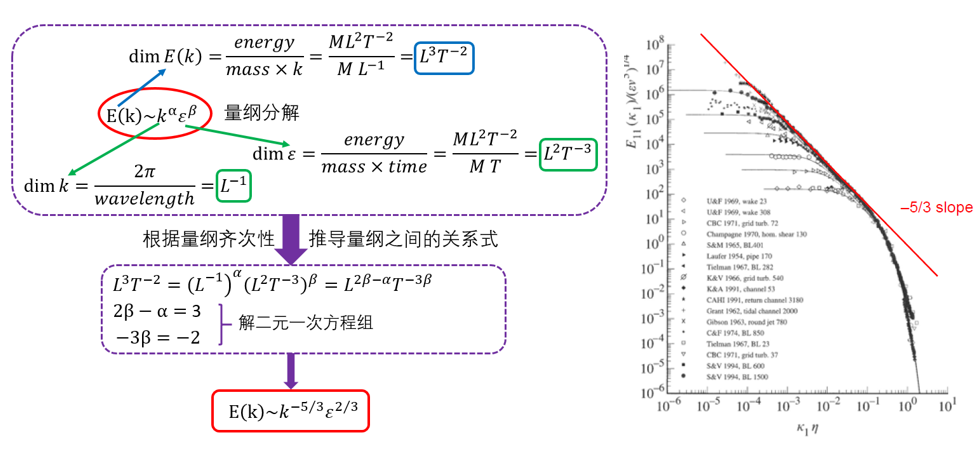
最后,柯大侠使出了一招平平无奇的量纲分析,在1941年提出了湍流世界最著名的-5/3幂律,并在众多学者的实验中得到了验证。当然随着湍流理论的不断发展,人们也发现了柯大侠的K41理论并非完美无缺,不过这并不妨碍它成为湍流研究史中最耀眼的一章。
“日月之行,若出其中;星汉灿烂,若出其里”,在令人眼花的CFD结果面前,湍流理论仍不动声色的掌控着局势。或许它也在等待,等待下一位大神的出现。
本文注明来源为其他媒体或网站的文/图等稿件均为转载,如涉及版权等问题,请作者在20个工作日之内联系我们,我们将协调给予处理。最终解释权归旭为光电所有。