昆明理工大学李俊昌教授研究团队在《激光与光电子学进展》发表题为“傍轴光学系统的相干光成像计算”的论文,被选为当期的封面文章。论文介绍了相干光成像系统像光场复振幅的精确计算公式及计算方法,该公式改写了50多年来国内外一成不变的只能近似计算像光场振幅分布的理论。论文以双透镜构成的成像系统为例,进行理论模拟及实验研究,证明了公式及其计算方法的正确性。
激光出现以后,相干光照明成像是一重要应用研究领域。顾德门教授[1]以单透镜成像系统为研究对象,基于线性系统理论及成像系统脉冲响应的近似,导出物体尺寸小于透镜直径1/4时可以计算像光场振幅分布的公式,并且,基于瑞利的成像理论,将透镜光瞳视为系统的出射光瞳,将像距视为出射光瞳到像平面的距离,公式被推广于多个元件构成的光学系统成像计算[1]。50多年来,该理论被国内外信息光学专著及教材广泛引用。然而,在相干光成像的应用研究中,像光场的振幅和相位通常是同等重要的物理量,建立准确的相干光照明成像理论逐渐成为必须解决的问题。
文献[2]推导出由2×2光学矩阵描述的成像系统像光场复振幅的计算公式,但公式的实验证明是采用单透镜构成的成像系统完成的[2],尚未给出多元件构成的成像系统的研究实例。文献[1]给出的像光场振幅分布计算公式虽然理论上可以推广于多个元件构成的成像系统,但也未看到这种推广的计算研究。
为此,昆明理工大学李俊昌教授研究团队对两种公式的计算方法进行了研究。对于任意给定的由2×2光学矩阵描述的成像系统,论文导出出射光瞳及出射光瞳到像平面距离的计算方法,并且,以两个透镜组成的成像系统为例,在不同空间位置放置孔径光阑,进行两种计算公式理论计算与实验测量的比较。研究结果表明,所导出的公式不受入射或出射光瞳尺寸的影响,能更准确地进行相干光成像计算。
设成像系统能由2×2元素的光学矩阵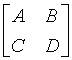 描述。定义直角坐标系O-xyz,令z轴与系统光轴重合,
描述。定义直角坐标系O-xyz,令z轴与系统光轴重合, 、
、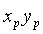 及
及 分别是系统的物平面、出射光瞳平面及像平面,出射光瞳函数为P(xp,yp),出射光瞳到像平面的距离为dpi。
由傅里叶变换及逆变换表示的像平面光波场表达式为[2]
分别是系统的物平面、出射光瞳平面及像平面,出射光瞳函数为P(xp,yp),出射光瞳到像平面的距离为dpi。
由傅里叶变换及逆变换表示的像平面光波场表达式为[2]
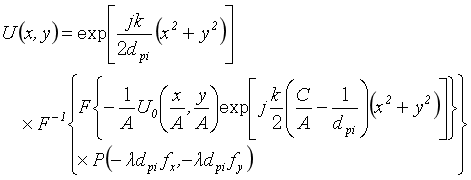 (1)
式中k=2π/λ,λ 为光波长,A 为像的横向放大率,fx,fy为频率空间坐标。
当物体尺寸小于透镜孔径1/4时,目前流行的计算像光场振幅分布的计算公式为[1]
(1)
式中k=2π/λ,λ 为光波长,A 为像的横向放大率,fx,fy为频率空间坐标。
当物体尺寸小于透镜孔径1/4时,目前流行的计算像光场振幅分布的计算公式为[1]
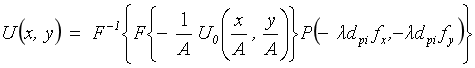 (2)
当光学系统及系统的孔径光阑位置及尺寸给定后, “傍轴光学系统的相干光成像计算”的论文基于矩阵光学理论,对以上两公式的计算方法进行讨论,获得了光学系统出射光瞳函数及出射光瞳到像平面距离的理论表达式。
(2)
当光学系统及系统的孔径光阑位置及尺寸给定后, “傍轴光学系统的相干光成像计算”的论文基于矩阵光学理论,对以上两公式的计算方法进行讨论,获得了光学系统出射光瞳函数及出射光瞳到像平面距离的理论表达式。
图1所示透镜L1及L2构成的成像系统为理论模拟及实验研究实例。
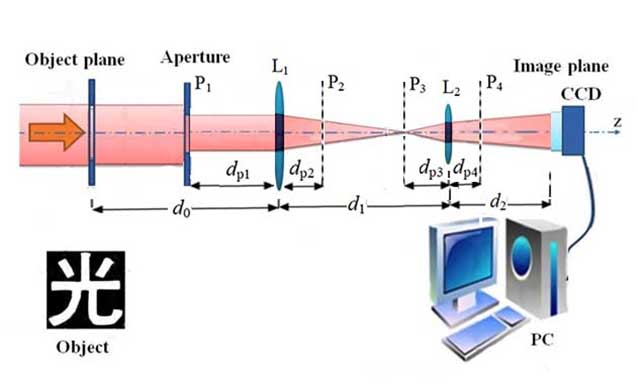
图中,用不透明的黑色有机玻璃板上刻出中文“光”字透光孔为物平面,照明物平面的是波长λ =633 nm的氦氖激光。激光经扩束和准直后成为沿光轴传播的平面波,放置在像平面的CCD探测器记录下像光场的强度分布。在实验研究中不同位置放置直径甚小于透镜孔径的圆孔光阑,同时用(1)式及(2)式计算像光场,并与实验测量进行比较。
实验系统的相关参数为:透镜L1的焦距f1=300 mm(孔径75 mm),透镜L2的焦距f2=157 mm(孔径30 mm),CCD的像素宽度dc=0.0052 mm(像素数量1024×1280),d0=328 mm,d1=435 mm。实验时用直径Dh=3.3 mm的圆孔光阑分别放在P1、P2、P3及P4位置(dp1=140 mm,dp2=150 mm,dp3=135 mm,dp4=55 mm,图1是圆孔光阑放在P1位置时的示意图)。
图2~图5给出孔径光阑分别放在P1、P2、P3及P4位置时的像平面光波场强度数值模拟与实验测量的比较。

图2 孔径光阑放置在P1位置时实验测量与理论模拟的比较。(a)CCD探测图像;(b)公式1理论模拟;(c)公式2理论模拟

图3 孔径光阑放置在P2位置时实验测量与理论模拟的比较。(a)CCD探测图像;(b)公式1理论模拟;(c)公式2理论模拟

图4 孔径光阑放置在P3位置时实验测量与理论模拟的比较。(a)CCD探测图像;(b)公式1理论模拟;(c)公式2理论模拟
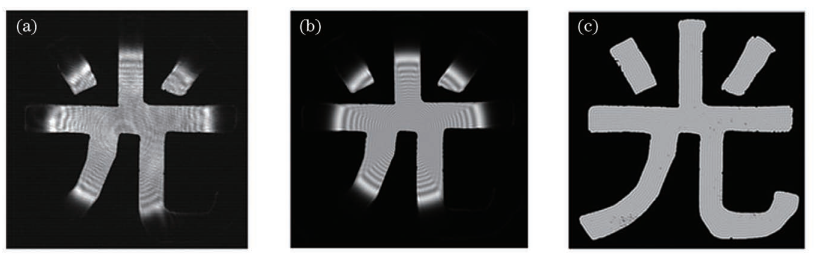
图5 孔径光阑放置在P4位置时实验测量与理论模拟的比较。(a)CCD探测图像;(b)公式1理论模拟;(c)公式2理论模拟
可以看出,式1的理论计算与实验测量吻合较好,只有在位置P3时(2)式的理论模拟才与实验测量相吻合。究其原因,是以上实验多数不满足物体尺寸小于入射光瞳1/4才能使用式2进行计算的条件[1],该使用条件在像空间的等价表述是:几何光学规定的物体像的尺寸必须小于出射光瞳直径的1/4。本实验中,将物体按照几何光学近似成像到像空间后,物体像的宽度约5 mm,在位置P3时出射光瞳直径为23.6 mm,满足使用公式2的条件。
应该指出,顾德门教授在推导公式2时,对单透镜成像系统的脉冲响应进行了简化及近似[1],导出的计算公式只能在特定的近似条件下计算像光场振幅分布。然而,相干光成像的像光场的振幅及相位分布在光学精密检测中通常是同等重要的物理量,公式1能为定量研究提供方便。
目前,非相干光成像的理论研究使用到相干光成像系统的脉冲响应[1],推导公式(1)时没有对脉冲响应作任何近似[2],若使用没有近似的复杂表达式进行研究,是否会对非相干光成像的理论研究结论产生影响,是需要进一步研究的课题。文献[2]对单色非相干光成像理论进行了研究,结果表明,对目前单色非相干光成像的理论不会产生影响。
相干光成像的像光场的振幅及相位分布在光学精密检测中通常是同等重要的物理量,公式1能为定量研究提供方便。然而,该公式是矩阵光学与菲涅耳衍射近似相结合导出的[2],为更准确地描述相干光成像,必须采用无傍轴近似的理论。此外,基于流行的近似计算公式2,出射光瞳定义的传递函数为理想像频谱的低通滤波器[1],然而,按照公式1,出射光瞳定义的传递函数的物理意义相似于理想像经过特定距离衍射的空间滤波器[3]。如何从理论上定量研究出射光瞳对成像质量的影响,将是科技工作者再深入研究的问题。
[1] Joseph W. Goodman著, 陈家璧, 秦克诚, 曹其智译. 傅里叶光学导论[M].第四版, 北京:科学出版社, 2020,151-153.
[2] 李俊昌, 熊秉衡. 信息光学教程[M]. 第二版, 北京: 科学出版社, 2017, 102-110.
[3] 李俊昌, 罗润秋, 彭祖杰, 宋庆和, 桂进斌, 夏海廷. 相干光成像系统传递函数的物理意义及实验证明[J]. 光学学报, 2021, 41(12):1207001.
云南省现代信息光学重点实验室于2020年底正式成立。该重点实验室是在传承了于1987成立的昆明理工大学“激光研究所”的历史积淀基础上,并经过了2016年成立的昆明理工大学“激光信息技术与应用重点实验室”的培育发展起来的。30多年来,在全息显示、衍射计算及数字全息研究领域形成特色,还开展了长期与法国三所工程师大学联合培养博士生的合作。
重点实验室成员先后主持国家级、省部级科研课题30余项;承办和主办国内外会议十多项;团队近年来在光信息处理领域编写了多部在国内外具有较大影响的专著和教材,如李俊昌教授的专著《衍射计算及数字全息》被列为“十二五”国家重点图书出版规划项目。重点实验室形成了以张亚萍、宋庆和、桂进斌、楼宇丽等年轻教授带头的研究团队,今后,将继续开展与发达国家的教学及科研合作,热切欢迎国内年轻才俊加入昆工的研究团队。

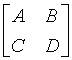 描述。定义直角坐标系O-xyz,令z轴与系统光轴重合,
描述。定义直角坐标系O-xyz,令z轴与系统光轴重合,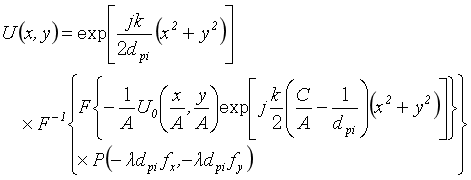 (1)
(1)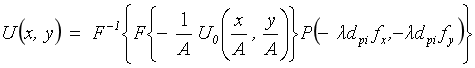 (2)
(2)










