APR: 深圳大学袁小聪教授团队在光学自旋斯格明子调控领域取得重要进展
撰稿|由课题组供稿
导读
研究背景
研究亮点
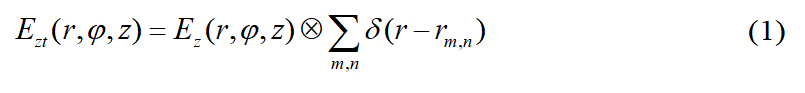
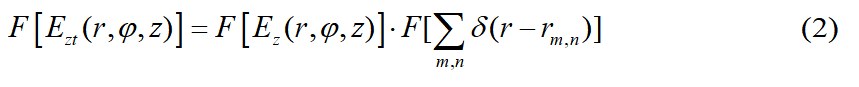
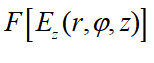 是单个圆偏SPP偶极子电场的傅里叶变换结果,它呈现为半径是波矢的圆环,而
是单个圆偏SPP偶极子电场的傅里叶变换结果,它呈现为半径是波矢的圆环,而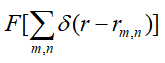 是二维晶格倒格子空间的格点。
是二维晶格倒格子空间的格点。
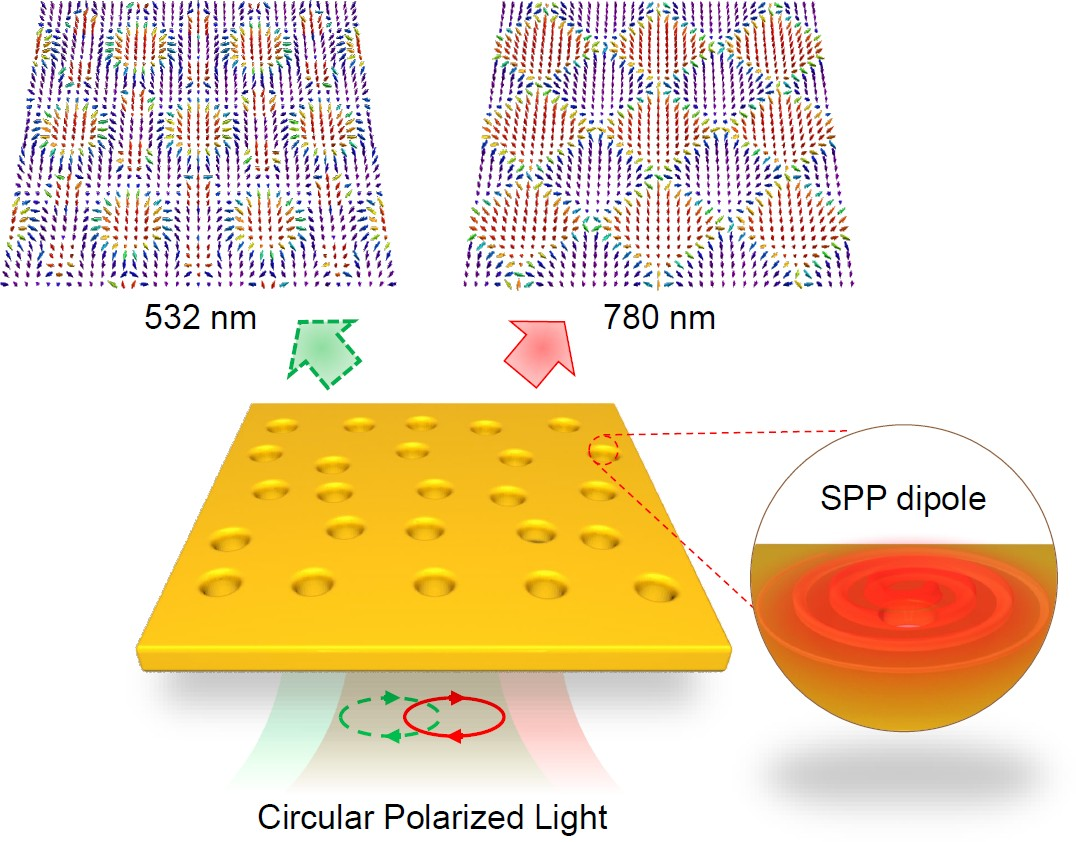
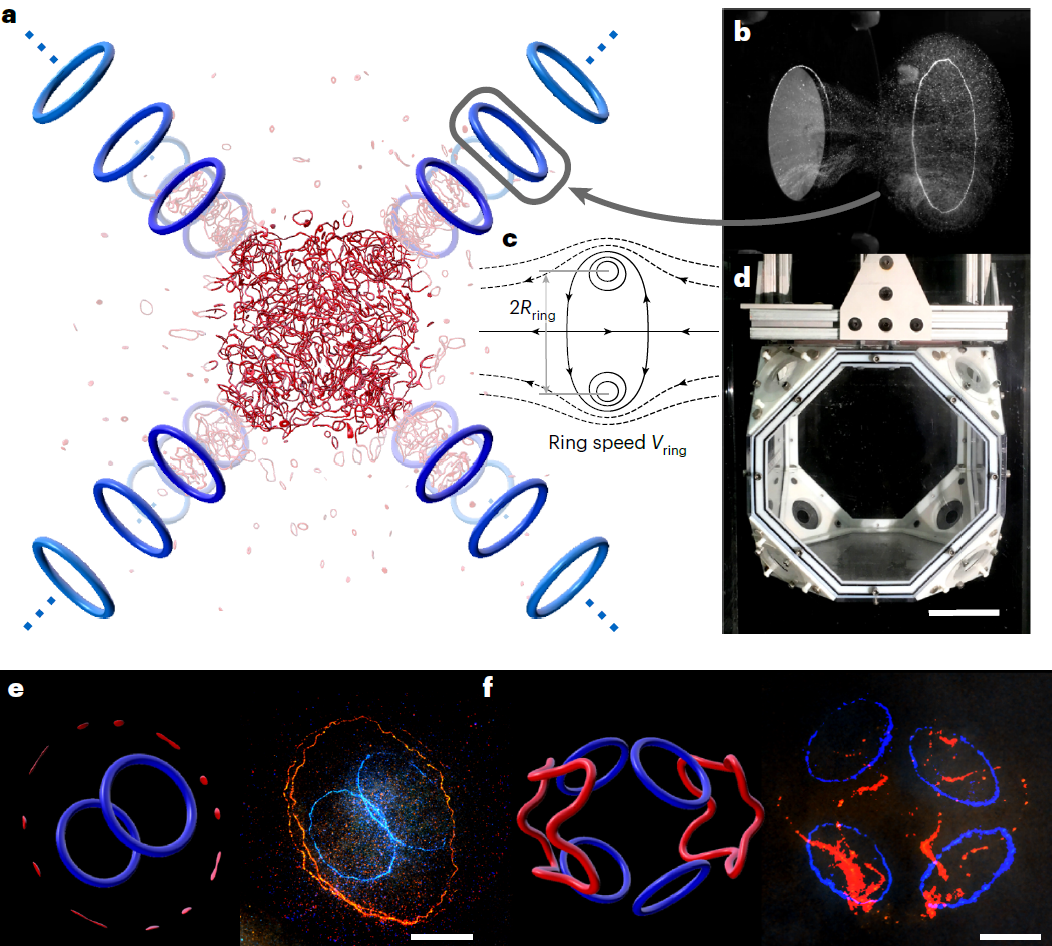
图1 不同自旋拓扑结构变换示意图。波长为532nm和780nm的圆偏振光可以在具有一定程度结构失序的金属纳米孔阵列表面分别激发光学自旋斯格明子和半子阵列。
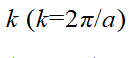 收缩到
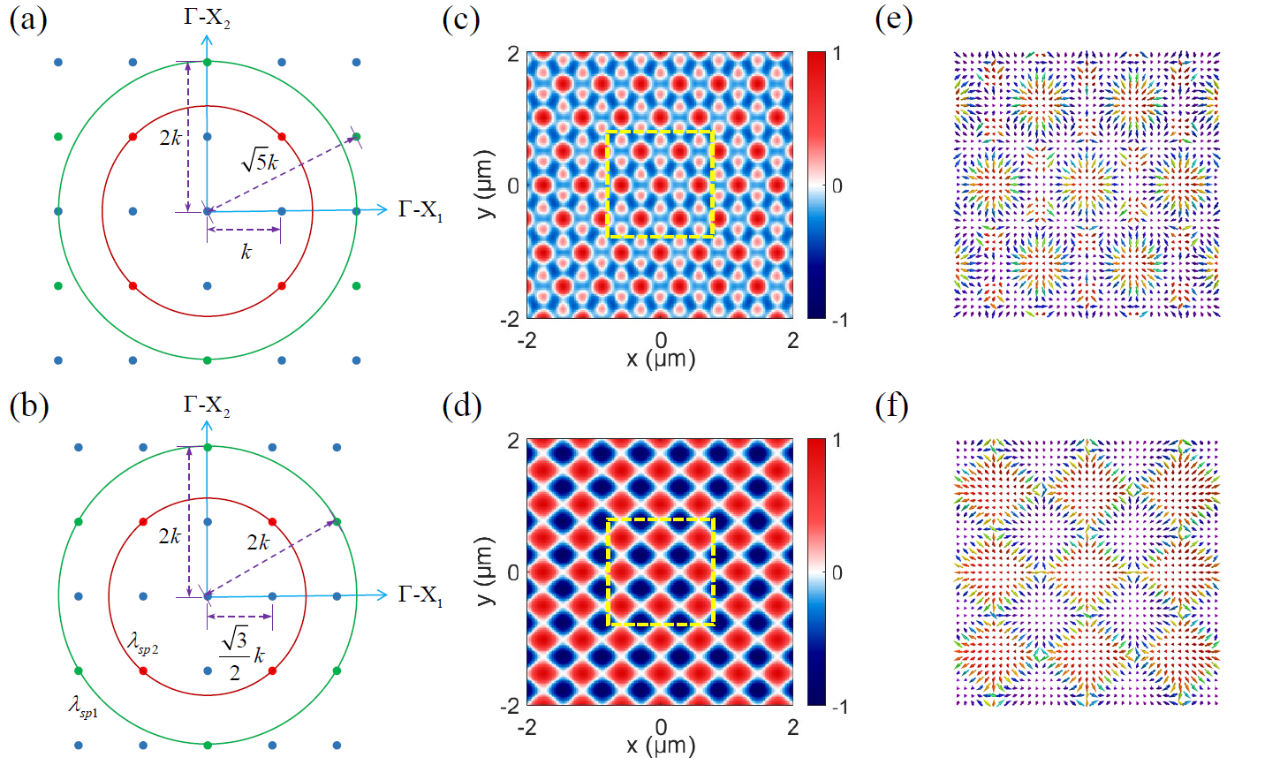
收缩到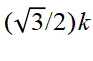 ,而Γ-X2方向的周期保持不变,如图2(b)所示,那么绿色和红色的圈将分别与六个和四个不同的倒格点重叠,其叠加后的光场分别呈六角和四角对称。在这种情况下,SPP波长分别满足
,而Γ-X2方向的周期保持不变,如图2(b)所示,那么绿色和红色的圈将分别与六个和四个不同的倒格点重叠,其叠加后的光场分别呈六角和四角对称。在这种情况下,SPP波长分别满足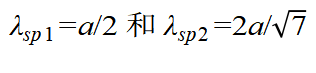 ,其光学自旋纵向分量Sz理论计算结果如图2(c)和(d)所示,自旋矢量分布如图2(e)和(f)所示,分别呈现光学斯格明子和半子阵列分布。而当SPP波长为其他特定数值时,与其他不同数目的倒格点重叠,与其对应的光学自旋纹理则会呈现其他各种不同的图案。
,其光学自旋纵向分量Sz理论计算结果如图2(c)和(d)所示,自旋矢量分布如图2(e)和(f)所示,分别呈现光学斯格明子和半子阵列分布。而当SPP波长为其他特定数值时,与其他不同数目的倒格点重叠,与其对应的光学自旋纹理则会呈现其他各种不同的图案。
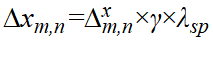 ,
,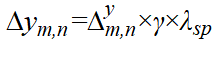 ,
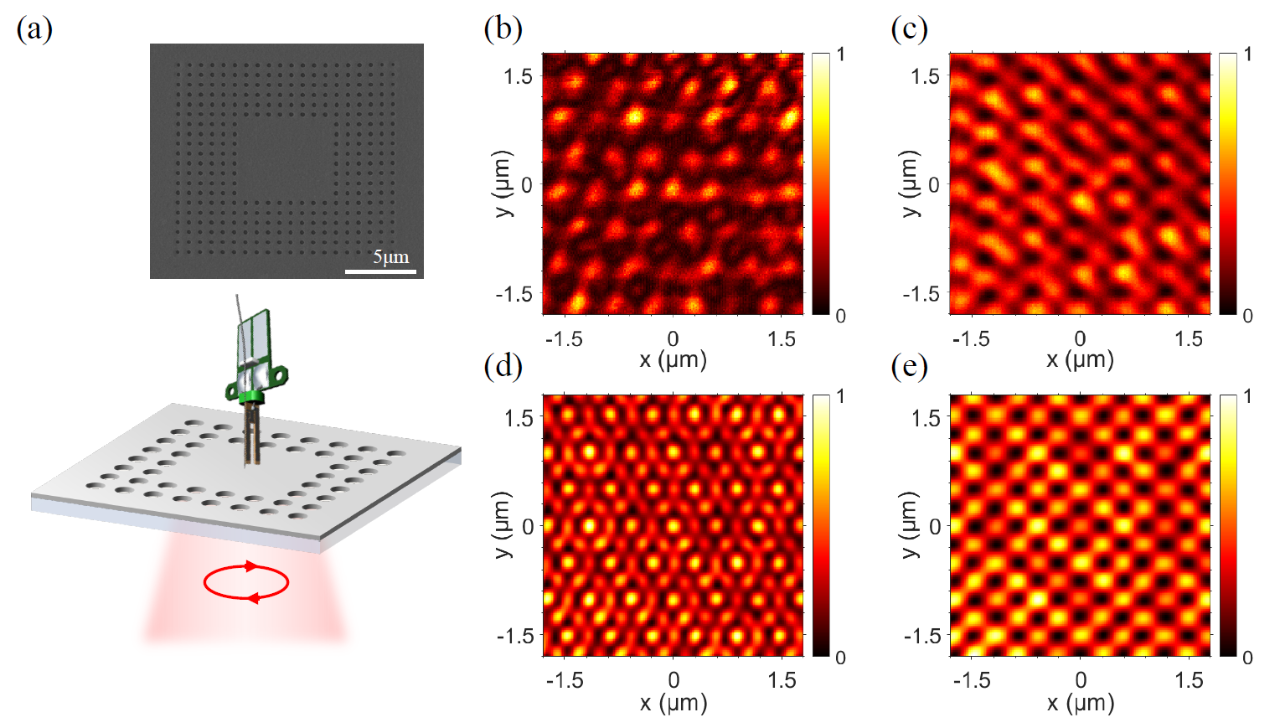
,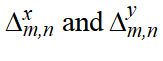 表示取值 −1到 +1之间的随机数,γ为随机程度,λsp表示SPP波长,当波长λ1的圆偏SPP偶极子叠加在每个格点上时,其相应的光学自旋纹理如图4所示。当γ从0不断增加到0.4时,虽然从图4中可以看到二维晶格的格点已变得有些混乱,但其相应的光学自旋纹理仍呈现规则的斯格明子阵列分布。而当γ增大到0.5时,光学自旋纹理才变得混乱。由此可见,随机程度γ存在一个阈值,在阈值以下,光学自旋纹理的分布具有高度稳定性。在阈值以上,光学自旋纹理的分布才变得混乱。当波长改为λ2时也有类似的结果。对于阈值的理论计算,可以对总场的傅里叶变换结果进行分析,判断
表示取值 −1到 +1之间的随机数,γ为随机程度,λsp表示SPP波长,当波长λ1的圆偏SPP偶极子叠加在每个格点上时,其相应的光学自旋纹理如图4所示。当γ从0不断增加到0.4时,虽然从图4中可以看到二维晶格的格点已变得有些混乱,但其相应的光学自旋纹理仍呈现规则的斯格明子阵列分布。而当γ增大到0.5时,光学自旋纹理才变得混乱。由此可见,随机程度γ存在一个阈值,在阈值以下,光学自旋纹理的分布具有高度稳定性。在阈值以上,光学自旋纹理的分布才变得混乱。当波长改为λ2时也有类似的结果。对于阈值的理论计算,可以对总场的傅里叶变换结果进行分析,判断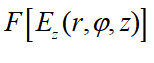 在什么情况下无法与倒格点进行重叠,从而推导出γ的阈值。
在什么情况下无法与倒格点进行重叠,从而推导出γ的阈值。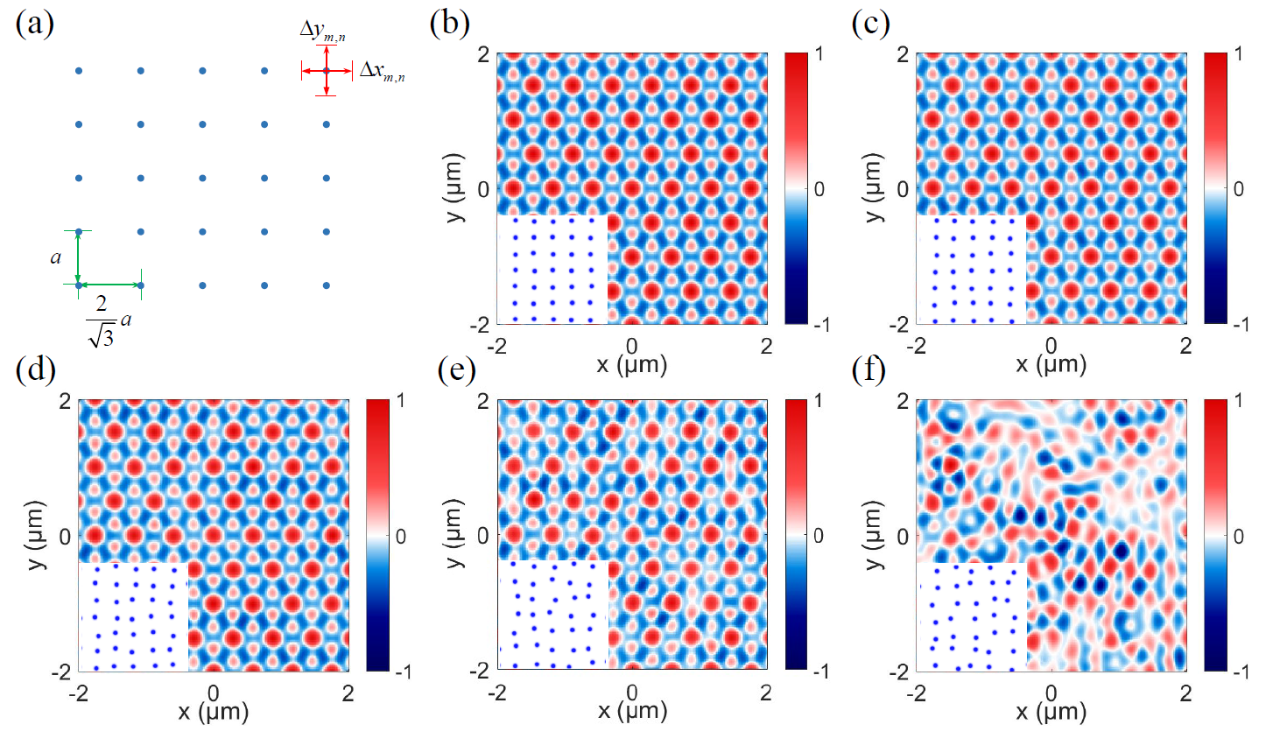
总结与展望
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。